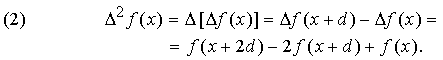11. Нахождение определителя матрицы по схеме Гаусса.

Определение:

Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы.

Пример решения:

12. Вычисление обратной матрицы по схеме Гаусса.

Определение:

Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы.

Общие шаги для вычисления:

Практически этот наиболее простой способ вычисления об­ратной матрицы состоит в следующих шагах.

1. К матрице А, по отношению к которой ищется обратная матрица, приписывается справа единичная матрица Е.

2. Путем преобразований методом Гаусса над строками рас­ширенной матрицы (А|Е) матрица А приводится к виду еди­ничной матрицы.

3. После окончания указанного вычислительного процесса, т. е. когда на месте исходной матрицы А будет сформирована единичная матрица, на месте приписанной справа единичной матрицы Е будет находиться обратная матрица А-1. Иными словами, вместо расширенной матрицы (А|Е) в итоге получaется расширенная матрица (E|A-1).

Пример решения:

13. Решение систем линейных уравнений методом итераций.

Определение:

Метод итерации — численный метод решения математических задач, приближённый метод решения системы линейных алгебраических уравнений. Суть такого метода заключается в нахождении по приближённому значению величины следующего приближения (являющегося более точным). Метод позволяет получить значения корней системы с заданной точностью в виде предела последовательности некоторых векторов(итерационный процесс). Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения корня x0.

Описание метода:

Условия сходимости процесса:

14. Метод квадратного корня. Метод Зейделя.

Метод квадратных корней для решения СЛАУ:

КВАДРАТНОГО КОРНЯ МЕТОД

- метод решения системы линейных алгебраич. уравнений А х= b с эрмитовой невырожденной матрицей А. Среди прямых методов он наиболее эффективен при реализации на ЭВМ.

Метод Гаусса—Зейделя - является классическим итерационным методом решения системы линейных уравнений.

15. Интерполяционная формула Лагранжа.

16. Конечные разности и интерполяционные формулы Ньютона.

Интерполяционные формулы Ньютона — формулы вычислительной математики, применяющиеся для полиномиального интерполирования.

Если узлы интерполяции равноотстоящие и упорядочены по величине, так что  , то есть  , то интерполяционный многочлен можно записать в форме Ньютона.

Интерполяционные полиномы в форме Ньютона удобно использовать, если точка интерполирования находится вблизи начала (прямая формула Ньютона) или конца таблицы (обратная формула Ньютона).

Первая интерполяционная формула Ньютона

Полученное выражение называется первой интерполяционной формулой Ньютона для интерполирования вперед.

Интерполяционную формулу обычно используют для вычисления значений функций в точках левой половины рассматриваемого отрезка. Это объясняется следующим.

Разности  ^kу_i вычисляются через значение функции у_i, у_{i +} , ..., у_{i + k}, причем i + k  n, поэтому при больших значениях i мы не можем вычислить разности высших порядков (k   n - i). Например, при i = n -  в можно учесть только  у,  ^у,  ^у.

Если в формуле положить n = 1 , то получим формулу линейной интерполяции:

P₁ (x) = у_t  у_.

При n = 2 будем иметь формулу квадратичной интерполяции:

P₂ (x) = у_t  у_ .

Вторая интерполяционная формула Ньютона

Формулу называют второй интерполяционной формулой Ньютона для интерполирования назад.

КОНЕЧНЫЕ РАЗНОСТИ. 

Исчисление конечных разностей связано с изучением свойств и применений разностей между соседними членами какой-нибудь последовательности или между значениями функции в точках, расположенных с постоянным интервалом в некотором пространстве. Слово «конечные» используется здесь в несколько устаревшем смысле «не бесконечно малые», т.е. не связанные с предельными переходами. Поскольку дифференциальное исчисление занимается изучением пределов разностей, а исчисление конечных разностей – самими разностями, то естественно, что между этими двумя теориями существуют много параллелей. Исчисления конечных разностей используются при интерполяции в математических таблицах, при суммировании числовых рядов, при вычислении интегралов и дифференцировании функций. Разности встречаются также в любой ситуации, когда надо описать поведение объекта, который испытывает воздействие меняющихся условий на определенном расстоянии (во времени и в пространстве). Например, термостату требуется значительное время, чтобы отреагировать на изменение температуры, поэтому он реагирует не на текущую температуру, а на ту, что была минуту назад. Другой пример: автомашиной управляет водитель, которому требуется какое-то время, чтобы отреагировать на возникшую на дороге ситуацию.

Под конечной разностью первого порядка функции f (x) принято понимать величину

где d – некоторая постоянная, которую часто, но не всегда, принимают равной 1. Разность второго порядка обозначается D2f и представляет собой разность разностей, т.е.