8. Оценка скорости сходимости метода итераций. Число итераций, необходимых для заданной точности.

Алгоритм решения системы Ax = b итерационными методами включает следующие этапы:

1. Для применения итерационных методов система должна быть приведена к эквивалентному виду x = Bx + d.

2. Выбирается начальное приближение к решению системы уравнений x(0)= (x10, x20, …, xm0).

3. Находится последовательность приближений к корню.

Для сходимости итерационного процесса достаточно, чтобы было выполнено условие . Критерий окончания итераций зависит от применяемого итерационного метода.

Число итераций  , необходимое для достижения заданной точности   определим из неравенства

 

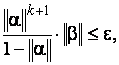
которое перепишем в виде:

При     получим:

Таким образом, необходимо не менее 11 итераций для достижения заданной точности приближённого решения. Однако, как указано ранее, это завышенная оценка. Поэтому будем вычислять последовательные приближения и оценивать погрешность каждого результата, используя неравенство в виде

9. Определение нормированного пространства. Примеры.

Нормированным векторным пространством называется векторное пространство с заданной на нем нормой.

Норма — функционал, заданный на векторном пространстве и обобщающий понятие длины вектора или абсолютного значения числа.

Примеры:

Линейные нормированные пространства

Любое предгильбертово пространство можно считать нормированным, так как скалярное произведение порождает естественную норму

Гёльдеровы нормы  -мерных векторов (семейство): ,

где   (обычно подразумевается, что это натуральное число).

В частности:

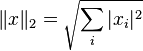 (евклидова норма),

 (это предельный случай  ).

Нормы функций в   — пространстве вещественных (или комплексных) непрерывных функций на отрезке [0,1]:

 — в смысле этой нормы пространство   непрерывных на отрезке функций образует полное линейное пространство. Этого нельзя сказать о следующих двух примерах нормы на этом пространстве, тем не менее, законных:

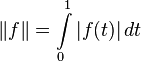
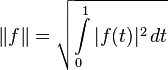
Аналогично можно ввести нормы для конечномерных векторных функций конечномерных векторных аргументов, заменив   на  , а интегрирование по отрезку интегрированием по области (максимум же на отрезке — в соответствующем случае — максимумом на области).

Некоторые виды матричных норм.

Порожденные нормы :

:  -норма, 

 (евклидова норма) и m = n (квадратные матрицы), подчиненная норма матрицы называется спектральная норма. Спектральная норма матрицы Aравна наибольшему сингулярному числу матрицы A или квадратному корню из наибольшего собственного числа положительно полуопределённой матрицы  :  , где   обозначает матрицу, сопряжённую к матрице  .

:  -норма 

Здесь   — сопряжённая к   матрица,   — след матрицы.

Поэлементная  -норма ( ): 

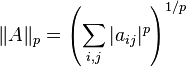
Норма Фробениуса: .

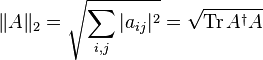
10 Решение систем линейных уравнений методом Гаусса.

Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы.

Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.

1. На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.

2. На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.

Метод Гаусса требует   арифметических операций.

Пример

Покажем, как методом Гаусса можно решить следующую систему:

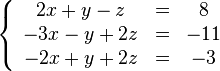
Обнулим коэффициенты при   во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на   и  , соответственно:

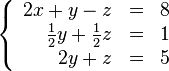
Теперь обнулим коэффициент при   в третьей строке, вычтя из неё вторую строку, умноженную на  :

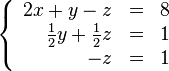
В результате мы привели исходную систему к треугольному виду, тем самым закончим первый этап алгоритма.

На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:

 из третьего;

 из второго, подставив полученное 

 из первого, подставив полученные   и  .

Таким образом исходная система решена.

В случае, если число уравнений в совместной системе получилось меньше числа неизвестных, то тогда ответ будет записываться в виде фундаментальной системы решений.