
- •1. Абсолютная и относительная погрешности. Десятичная запись, значащая цифра, число верных знаков.
- •Или можно записать
- •2. Общая формула для погрешности
- •3. Основные требования предъявляемые к вычислительным алгоритмам. Устойчивость. Точность. Эффективность. Экономичность. Аварийные остановы.
- •4. Отделение корней. Графическое решение уравнений. Метод половинного деления.
- •5. Метод касательных. Метод хорд. Оценка приближения.
- •6. Метод хорд. Оценка приближения.
- •7. Метод итераций. Теорема Банаха.
- •8. Оценка скорости сходимости метода итераций. Число итераций, необходимых для заданной точности.
- •9. Определение нормированного пространства. Примеры.
- •10 Решение систем линейных уравнений методом Гаусса.
- •11. Нахождение определителя матрицы по схеме Гаусса.
- •12. Вычисление обратной матрицы по схеме Гаусса.
- •13. Решение систем линейных уравнений методом итераций.
- •14. Метод квадратного корня. Метод Зейделя.
- •15. Интерполяционная формула Лагранжа.
- •16. Конечные разности и интерполяционные формулы Ньютона.
- •17. Формулы приближенного дифференцирования, основанные на первой интерполяционной формуле Ньютона.
- •18. . Формула прямоугольников. Формула трапеций. Оценки погрешности.
- •19. Формула Симпсона. Оценки погрешности. Метод парабол (Симпсона)
- •20.Обычный алгоритм Монте-Карло интегрирования
- •21. Решение задачи Коши для дифференциальных уравнений методом Эйлера.
- •22. Решение задачи Коши для дифференциальных уравнений методом Рунге-Кутта.
- •23. Общая схема метода Галеркина для решения уравнений
- •24. Решение краевой задачи для дифференциальных уравнений методом Галеркина.
5. Метод касательных. Метод хорд. Оценка приближения.
Метод Ньютона (метод касательных)
Расчетная формула метода Ньютона имеет вид:
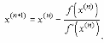
Геометрически метод Ньютона означает, что следующее приближение к корню x^(n+1) есть точка пересечения с осью ОХ касательной, проведенной к графику функции y = f(x) в точке (x^(n), f(x^(n))).
Теорема о сходимости метода Ньютона
Пусть
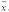 простой корень уравнения f(x)=0,
в некоторой окрестности которого
функция дважды непрерывно дифференцируема.
Тогда найдется такая малая σ
- окрестность корня
,
что при произвольном выборе
простой корень уравнения f(x)=0,
в некоторой окрестности которого
функция дважды непрерывно дифференцируема.
Тогда найдется такая малая σ
- окрестность корня
,
что при произвольном выборе
начального приближения x^(0) из этой окрестности итерационная последовательность метода Ньютона не выходит за пределы окрестности и справедлива оценка
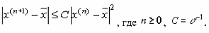
Критерий окончания итерационного процесса: при заданной точности > 0 вычисления следует вести до тех пор пока не окажется выполненным неравенство
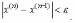
Как указано в теореме, метод Ньютона обладает локальной сходимостью, то есть областью его сходимости является малая окрестность корня . Неудачный выбор может дать расходящуюся итерационную последовательность.
Метод Хорд. (метод уточнения корней)
Для
реализации данного метода нужно построить
исходную функцию
и найти значение функции на концах
отрезка
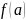 и
и
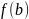 .
Затем провести хорду M1M2
с концами в точках M1(a,
f(a)), M2(b,
f(b)). Абсцисса
точки пересечения с осью ОХ это и есть
приближенный корень
.
Затем провести хорду M1M2
с концами в точках M1(a,
f(a)), M2(b,
f(b)). Абсцисса
точки пересечения с осью ОХ это и есть
приближенный корень
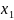 .
Далее найти точку M3(
,
f(
)).
Построить следующую хорду и найти второй
приближенный корень
.
Далее найти точку M3(
,
f(
)).
Построить следующую хорду и найти второй
приближенный корень
 .
И так далее. В зависимости от поведения
функции возможны два случая:
.
И так далее. В зависимости от поведения
функции возможны два случая:
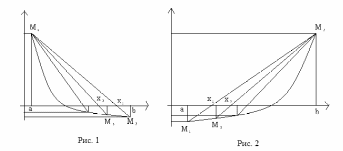
Для первого случая (рис. 1), справедлива следующая формула:

И
справедливо неравенство: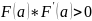 ,
где
,
где
 ;
;
Для второго случая (рис.2) справедлива следующая формула:

И
справедливо неравенство: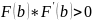 ,
где
,
где
 ;
;
Условия сходимости метода аналогичны условиям сходимости метода Ньютона.
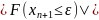
6. Метод хорд. Оценка приближения.
Метод Хорд. (метод уточнения корней)
Для реализации данного метода нужно построить исходную функцию и найти значение функции на концах отрезка и . Затем провести хорду M1M2 с концами в точках M1(a, f(a)), M2(b, f(b)). Абсцисса точки пересечения с осью ОХ это и есть приближенный корень . Далее найти точку M3( , f( )). Построить следующую хорду и найти второй приближенный корень . И так далее. В зависимости от поведения функции возможны два случая:
Для первого случая (рис. 1), справедлива следующая формула:
И справедливо неравенство: , где ;
Для второго случая (рис.2) справедлива следующая формула:
И справедливо неравенство: , где ;
Условия сходимости метода аналогичны условиям сходимости метода Ньютона.
7. Метод итераций. Теорема Банаха.
Метод простой итерации (метод последовательных повторений)
Для применения метода простой итерации следует исходное уравнение f(x) = 0 преобразовать к виду, удобному для итерации x = φ(x). Это преобразование можно выполнить различными способами. Функция φ (x) называется итерационной функцией. Расчетная формула метода простой итерации имеет вид:
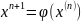
Теорема о сходимости метода простой итерации.
Пусть в
некоторой σ – окрестности корна
функция
 дифференцируема и удовлетворяет
неравенству
дифференцируема и удовлетворяет
неравенству
 ,
где
,
где
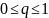 – постоянная. Тогда независимо от выбора
начального приближения из указанной
σ – окрестности иррациональной
последовательности не выходит из
окрестности, метод сходится со скоростью
геометрической последовательности и
справедлива оценка погрешности:
– постоянная. Тогда независимо от выбора
начального приближения из указанной
σ – окрестности иррациональной
последовательности не выходит из
окрестности, метод сходится со скоростью
геометрической последовательности и
справедлива оценка погрешности:

Критерий окончания итерационного процесса. При заданной точности ε >0 вычисления следует вести до тех пор, пока не окажется выполненным неравенство

Если величина 0 <q<0,5, то можно использовать более простой критерий окончания итераций:

Внимание. Ключевым моментом в применении метода простой итерации является эквивалентное преобразование уравнения к новой форме. Способ, при котором выполнено условие сходимости метода простой
итерации, состоит в следующем:
исходное уравнение приводится к виду x = x - α f(x). Предположим дополнительно, что производная f’ непрерывна и
положительна на заданном отрезке, т.е. справедливо выполнение неравенства m ≤ f’(x) ≤ M на отрезке [a,b]. Тогда при выборе итерационного параметра α = 2/(m+M) метод сходится и значение

Если же известна для производной только оценка сверху, то положим α = 1/ M и q = 1 – m/M – тоже менее единицы.
