3. Основные требования предъявляемые к вычислительным алгоритмам. Устойчивость. Точность. Эффективность. Экономичность. Аварийные остановы.

Точность. Обозначим через y точное решение задачи, yk – ее приближенное значение, полученное на k-м шаге численного метода. Тогда

Dy = y - yk

составляет погрешность решения, а

D = Dy = y - yk

является абсолютной погрешностью.

Вычислительный алгоритм должен давать решение с заданной точностью e1 и, следовательно, критерием завершения процесса уточнения решения является выполнение неравенства

D = y - yk ≤ e1 .

Эффективность. Эффективность вычислительного алгоритма оценивают по времени реализации либо по общему числу операций,требуемых для получения результата.

Обозначим через nсл число операций сложения, через nу – число операций умножения, через nдел – число операций деления, через tу, tдел,tсл – время выполнения операций умножения, деления и сложения на ЭВМ. Объективный критерий сравнения вычислительных алгоритмов– требуемое время вычислений:

T=nу·tу+nсл·tсл+nдел·tдел.

Если tу ≈ tдел ≈ tсл,

то T ≈ (nу+nдел+nсл)tоп,

где tоп – время выполнения на ЭВМ арифметической операции,

и критерием оценки эффективности алгоритма может быть

nΣ=nу+nдел+nсл .

Если tу≈tдел>>tсл, то критерий эффективности – число так называемых длинных операций nдл=nдел+nу.

Экономичность. Экономичность алгоритма оценивается по требуемым для его реализации объемам памяти ЭВМ. Экономичность вычислительного алгоритма, т.е. минимизация числа элементарных операций при выполнении его на ЭВМ.

Аварийные остановы. Любое число ЭВМ принадлежит не всей числовой оси, а некоторому интервалу (M0,M∞ ) . Если какое-либо число x в процессе работы алгоритма выходит за указанный интервал, то происходит так называемый аварийный останов. Необходимо построить вычислительный алгоритм таким образом, чтобы вычисленные

в процессе его работы числа x (M0,M∞ ) .

4. Отделение корней. Графическое решение уравнений. Метод половинного деления.

Пусть рассматривается уравнение . Корнем уравнения называется 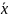, при которой .

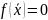Корень называется простым, если , в противном случае корень называется кратным. Кратное число m называется кратностью корня , если для k=1,2,3-,m-1 и .

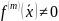Постановка задачи. Вычисление приближенного значения корня с

Точностью предполагает поиск найти такое значения x , что

Отделение корней, теорема:

Если функция 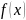, определяющая уравнение , на концах отрезка [a,b] принимает значенияfразных знаков, т.е. f(a)*f(b)<0, то на этом отрезке содержится, по крайней мере один корень уравнения.

Если функция f(x) строго монотонна, то корень на [a,b] единственный (f’(a)*f”(b)>0)

Решение задачи разбивается на два этапа:

 на первом этапе осуществляют локализацию корней,

 на втором этапе производят итерационное уточнение корней.

На этапе локализации корней находят достаточно узкие отрезки (или отрезок, если корень единственный), которые содержат один и только один корень уравнения f(x)=0. На втором этапе вычисляют приближенное значение корня с заданной точностью. Часто вместо отрезка локализации достаточно указать начальное приближение к корню.

Метод дихотомии (деления отрезка пополам)

Пусть [a,b] – отрезок локализации. Предположим, что функция f(x) непрерывна на [a,b] и на концах принимает значения разных знаков, т.е. f(a) * f(b) < 0.

Алгоритм метода дихотомии состоит в построении последовательности вложенных отрезков, на концах которых функция принимает значения разных знаков. Каждый последующий отрезок получают делением пополам

предыдущего. Опишем один шаг итераций метода.

Пусть на k-ом шаге найден отрезок

Такой, что

Найдем середину отрезка

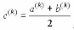
Если 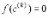, то корень и задача решена.

Если нет, то из двух половин отрезка выбираем ту, на концах которой функция имеет противоположные знаки:

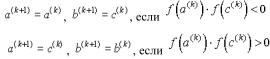
Критерий окончания итерационного процесса: если длина отрезка локализации меньше 2ε, то итерации прекращают и в качестве значения корня с заданной точностью принимают середину отрезка.