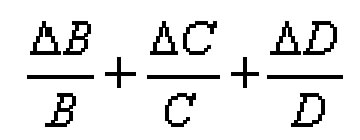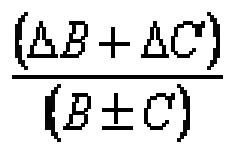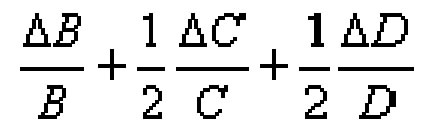Или можно записать

если считать, что величина Δx является знаковой, то есть, может быть как положительным, так и отрицательным числом, потому что x может быть приближением как по недостатку, так и по избытку. Обозначим абсолютную погрешность функции через Δy

Ввиду малости Δx мы можем заменить приращение функции ее дифференциалом.

Тогда получим

Что и требовалось доказать.

Рассмотрим относительную погрешность вычисления функции одной переменной.

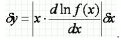
В таком виде выражение удобно для приложения к легко логарифмируемым функциям.

Абсолютная и относительная погрешность вычисления функции нескольких переменных

Абсолютная погрешность результата вычисления функции нескольких приближенных чисел равна сумме произведений модуля частной производной функции на абсолютную погрешность приближенного числа.

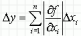
Для относительной погрешности вычисления функции нескольких приближенных чисел получим выражение, так же аналогичное случаю функции одной переменной:

Абсолютная и относительная погрешность вычисления суммы и разности приближенных чисел

предельная абсолютная погрешность как суммы, так и разности нескольких приближенных чисел равна сумме предельных абсолютных погрешностей слагаемых.

При определении относительной погрешности суммы и разности результаты будут различны.

Итак, для оценки погрешности мы получили следующие простые правила:

 При сложении и вычитании абсолютные погрешности складываются;

 При умножении и делении относительные погрешности складываются;

 При возведении в степень относительные погрешности умножаются на абсолютную величину показателя степени;

 При отыскании значения функции абсолютная погрешность функции равна произведению абсолютной погрешности аргумента на абсолютную величину производной

2. Общая формула для погрешности

Выполнение лабораторных работ связано с измерением различных физических величин и последующей обработкой их результатов.    Измерение ― нахождение значения физической величины опытным путем с помощью средств измерения.    Прямое измерение — определение значения физической величины непосредственно средствами измерения.    Косвенное измерение — определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемыми прямыми измерениями.     При любом измерении всегда неизбежна большая или маленькая погрешность.    Абсолютная погрешность (Δ) — абсолютное значение погрешности.    Для оценки точности измерения надо знать, какую часть измеряемой величины составляет абсолютная погрешность, допущенная при измерении, это число называется относительной погрешностью (e).   Пусть  А, В, С,…— физические величины             Апр — приближённое значение физической величины, то есть значение полученное путем прямых или косвенных измерений.             ΔА — абсолютная погрешность измерения физической величины.             εА — относительная погрешность измерения физической величины. εА = ΔА/Апр*100% ΔА (в большинстве случаев) равна цене деления прибора. ΔА обычно округляют до одной значащей цифры: ΔА = 0,17 ≈ 0,2. Апр округляют так, чтобы его последняя цифра оказалась в том же разряде, что и цифра погрешности: Апр= 10,332 » 10,3. Относительная погрешность косвенныхизмерений определяется с помощью формул:

№ п/п	Формула физической величины	Формула относительной погрешности
1	А= В*С*D	e =
2	А=   *D
3	A= B ± C	e =
4	А = В*С2	e = ΔB/B + 2*ΔC/C
5	A = B*	e =

Абсолютная погрешность косвенных измерений ∆А = εА* Апр (e- выражается десятичной дробью)   Ответ записывается в форме:         А = Апр ±  ΔА