24. Решение краевой задачи для дифференциальных уравнений методом Галеркина.

Рассмотрим в качестве иллюстрации обыкновенное дифференциальное уравнение:

с граничными условиями:

Решение данного уравнения известно:

Для первого нетривиального решения   собственное число равно  .

Теперь применим метод Галёркина. Выберем сперва одну базисную функцию:

Подставляя в уравнение, получим невязку:

и требование ортогональности невязки перепишется в виде:

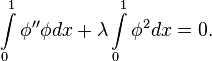
Отсюда очевидно:

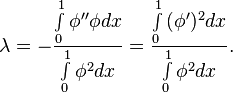
В приводимом здесь примере получается  , что менее чем на 1,5 % отличается от точного решения. Задание большего числа базисных функций позволяет уточнить уже известное значение λ, а также получить первое приближение для следующего (соответствующего n=2).

Представим решение в виде линейной комбинации n функций:

Тогда невязка:

.

Система уравнений для коэффициентов разложения:

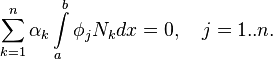
В этом случае собственные значения находятся из условия разрешимости системы (равенство нулю её определителя):

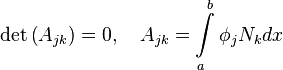
Важно помнить, что сходимость метода Галёркина не всегда быстро достигается. Успешное применение возможно только для т. н. самосопряжённых задач, то есть инвариантных к эрмитовому сопряжению.