22. Решение задачи Коши для дифференциальных уравнений методом Рунге-Кутта.

Метод Рунге-Кутта

Данный метод является одним из наиболее распространенных численных методов интегрирования обыкновенных дифференциальных уравнений. По сравнению с описанным выше методами Эйлера метод Рунге-Кутта имеет более

высокую точность.

Пусть на отрезке [a, b] требуется найти численное решение задачи Коши y′ = dy(t)/dt = f (y, t)

с соответствующим начальным условием

y₀ = y(t ₀ )

, где a = t ₀ . Как и в предыдущем методе разобьем этот участок на n равных частей и построим последовательность значений t ₀ , t ₁ , t ₂ , …, t _n аргумента t искомой функции y(t). Предполагаем существование непрерывных производных функции y(t) до пятого порядка.

Формулу для решения можно записать в виде:

y _k+1 = y _k + ∆y _k

где ∆y _k — приращение искомой функции y(t) на (k+1)-ом шаге интегрирования.

Придадим аргументу t приращение, равное шагу интегрирования h, и разложим функцию y(t + h) в ряд Тейлора в окрестности точки t, сохранив в нем пять членов:

Перенося первое слагаемое в этой сумме в левую часть получим, что

Здесь производные 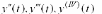определяются последовательным дифференцированием уравнения y = y (t)

Вместо непосредственных вычислений по формуле (10.6) в методе Рунге-Кутта для каждого значения ∆y _k = ∆ y(x _k ) определяются четыре числа:

Доказывается, что если числа k 1k , k 2k , k 3k , k 4k , последовательно умножить на 1/6, 1/3, 1/3, 1/6 и сложить между собой, то выражение (10.10), соответствующее формуле Рунге-Кутта:

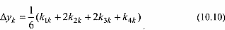
имеет погрешность R _n (h⁵).

Таким образом, рабочая формула Рунге-Кутта для интегрирования имеет вид:

Метод Рунге-Кутта может быть использован и при решении систем дифференциальных уравнений.

23. Общая схема метода Галеркина для решения уравнений

Метод Галёркина (метод Бубнова — Галёркина) — метод приближённого решения краевой задачи для дифференциального уравнения  . Здесь оператор   может содержать частные или полные производные искомой функции.

Краевая задача — дифференциальное уравнение (система дифференциальных уравнений) с заданными линейными соотношениями между значениями искомых функций на начале и конце интервала интегрирования.

Решение краевой задачи ищется в виде линейной комбинации решений однородных задач Коши, соответствующих заданному уравнению при линейно независимых векторах начальных условий, и решения неоднородной задачи Коши с произвольными начальными условиями.

Пример краевой задачи:

Первым шагом в реализации метода Галёркина является выбор набора базисных функций, которые:

- удовлетворяют граничным условиям.

- в пределе бесконечного количества элементов базиса образуют полную систему.

Конкретный вид функций определяется из специфики задачи и удобства работы. Часто применяются тригонометрические функции, ортогональные полиномы (полиномы Лежандра, Чебышёва, Эрмита и др.).

Решение представляется в виде разложения по базису:

Затем приближённое решение подставляется в исходное дифференциальное уравнение, и вычисляется его невязка. Для однородного уравнения:

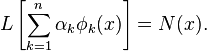
Для неоднородного уравнения L[u]=f(x) невязка будет иметь вид N(x)=L[u]-f(x)

Далее выдвигается требование ортогональности невязки к базисным функциям, то есть:

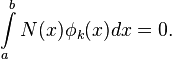
Отсюда получается однородная система уравнений для коэффициентов в разложении, и удаётся приближённо найти собственные значения задачи.