4Микро и макро состояние. Статический вес.

Микросостояние — это состояние системы, определяемое одновременным заданием координат и импульсов всех составляющих систему частиц. Знание микросостояния в некоторый момент времени позволяет однозначно предсказать эволюцию системы во все последующие моменты.

Макросостояние — это состояние системы, характеризуемое небольшим числом макроскопических параметров. Одно макросостояние может быть реализовано большим числом микросостояний за счет перестановки частиц, не меняющей наблюдаемого состояния.

Статистическое описание больших систем существенно опирается на следующие постулаты.

1. Все разрешенные микросостояния равновероятны.

2. Термодинамически равновесным является то макросостояние, которое реализуется наибольшим числом микросостояний, т. е. является наиболее вероятным состоянием.

Статисти́ческий вес — физическая величина, определяющая в квантовой механике и квантовой статистике количество различных квантовых состояний системы с одинаковой энергией (синоним: кратность вырождения энергетического уровня). В статистической физике и термодинамике статистическим весом называют количество способов (микросостояний системы), которыми может быть реализовано данное макроскопическое состояние статистической системы. Статистический вес обычно обозначается символами Γ, g, w, W или Ω.

По вышеприведённому определению, статистический вес является безразмерным целым числом, большим или равным единице,   Иногда статвес называют термодинамической вероятностью, хотя необходимо отметить, что вероятность обычно определяется как действительное число в интервале от 0 до 1.

При рассмотрении квантовых систем с непрерывным спектром энергии под статистическим весом обычно понимают количество квантовых состояний, приходящихся на определённый энергетический интервал. В таком определении статвес имеет размерность обратной энергии.

24.

Температура и поступательные степени свободы.

Числом степеней свободы материального объекта называют число независимых координат, которые необходимо задать, чтобы однозначно определить положение этого объекта относительно рассматриваемой системы отсчета.  Например, положение материальной точки в пространстве определяется тремя координатами x, y, z, следовательно, материальная точка обладает тремя степенями свободы.  Две материальные точки, находящиеся на неизменном расстоянии друг от друга (например, модель двухатомной молекулы с жесткой связью между атомами) , имеют пять степеней свободы – три поступательные и две вращательные. Таким образом, двухатомная молекула может совершать пять независимых движений: три поступательных движения вдоль осей X, Y, Z и два вращения относительно осей X и Y (рис. 1). Опыт показывает, что вращение относительно оси Z, на которой лежат центры обоих атомов, может быть возбуждено только при очень высоких температурах. При обычных температурах вращение около оси Z не происходит, так же как не вращается одноатомная молекула.  Рис. 1.  Каждое независимое движение называется степенью свободы. Таким образом, одноатомная молекула имеет 3 поступательные степени свободы, «жесткая» двухатомная молекула имеет 5 степеней (3 поступательные и 2 вращательные) , а многоатомная молекула – 6 степеней свободы (3 поступательные и 3 вращательные) . 

При достаточно высоких температурах в многоатомных молекулах возбуждаются дополнительные – колебательные степени свободы, связанные с изменением расстояний между атомами. Например, в двухатомной молекуле при данных условиях насчитывается 6 стпеней свободы (3 поступательные, 2 вращательные и 1 колебательная) . 

25.

Скорость движения молекул газа.

Скорость движения молекул в теле связана с его температуре и: чем больше эта скорость, тем выше температура тела. Таким образом, скорость движения молекул определяет тепловое состояние тела - величину его внутренней энергии; поэтому хаотическое движение молеку л также называют тепловым движением. [1]

Скорости движения молекул в газах и жидкостях почти одинаковы, однако в газе молекулы проходят значительно большее расстояние, прежде чем столкнуться ( вследствие более низкой плотности), поэтому коэффициенты диффузии в газе в 105 - 106 раз выше, чем в жидкости. Этот факт получает отражение в пропорциональности между Dg и величиной, обратной давлению в системе. Результатом любого диффузионного процесса с участием молекул, имеющих различную массу, является массообмен через некоторую плоскость в системе, причем наличие градиента плотности усложняет процесс конвективного смешивания. В газах этот эффект мал и коэффициент диффузии почти не зависит от концентрации вещества. Это обстоятельство делает возможным использование в ГХ коэффициентов диффузии в газовой фазе Dg для надежного определения диффузионных эффектов. [3]Скорость движения молекулы прямо пропорциональна ее кинетической энергии. Чем быстрее движется молекула, тем выше ее кинетическая энергия. [10]

26

Число степеней свободы

Числом степеней свободы механической системы называется количество независимых величин, с помощью которых может быть задано положение системы в пространстве.

Положение материальной точки в пространстве определяется значениями трёх её координат, например декартовых координат x, y, z

27

Давление идеального газа

Идеальный газ - модель реального газа, которая удовлетворяет следующим требованиям:

• Расстояние между молекулами гораздо больше их размеров (молекулы можно считать материальными точками);

• Силами взаимодействия, кроме моментов соударения, можно пренебречь (потенциальная энергия взаимодействия молекул по сравнению с кинетической энергией хаотического движения пренебрежимо мала);

• Столкновение молекул друг с другом и со стенками абсолютно упругое;

• Движение каждой молекулы подчиняется классическим законам динамики Ньютона.

Реальный разреженный газ приблизительно ведет себя как идеальный газ.

Давление идеального газа пропорционально концентрации молекул и средней кинетической энергии их поступательного движения.

Давление, температура и объем - параметры состояния газа. Или их называют макропараметрами. Температура - внешняя характеристика скоростей частиц газа. Давление - внешняя характеристика соударений со стенками, например, сосуда. Объем - место, куда заключены частицы газа. Газ занимает весь предоставленный ему объем. Существуют еще внешние параметры, например тела или поля, действующие на газ из вне.

28.

Уровнение состояния идеального газа

p = nkT,

связывающее давление газа с его температурой и концентрацией молекул, получено в §3.2 для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений

Произведение постоянной Авогадро N_А на постоянную Больцмана k называется универсальной газовой постоянной и обозначается буквой R. Ее численное значение в СИ есть: 

R = 8,31 Дж/моль·К.

Соотношение 

(*)

называется уравнением состояния идеальногъо газа.

29

Реальные газы . Уравнение идеального газа

Согласно модели Ван-дер-Ваальса, силы притяжения между молекулами (силы Ван-дер-Ваальса) обратно пропорциональны шестой степени расстояния между ними, или второй степени объема, занимаемого газом. Считается также, что силы притяжения суммируются с внешним давлением. С учетом этих соображений уравнение состояния идеального газа преобразуется в уравнение Ван-дер-Ваальса:

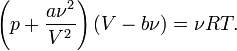
Предпринималось много попыток для учета отклонений свойств реальных газов от свойств идеального газа путем введения различных поправок в уравнение состояния идеального газа

30.

Фазовые диограммы

Фа́зовая диагра́мма (диаграмма состоя́ния) — графическое отображение равновесного состояния бесконечной физико-химической системы при условиях, отвечающих координатам рассматриваемой точки на диаграмме (носит название фигуративной точки).

Классификация фазовых переходов При фазовом переходе первого рода скачкообразно изменяются самые главные, первичные экстенсивные параметры: удельный объём (т.е. плотность), количество запасённой внутренней энергии, концентрация компонентов и т. п. Подчеркнём: имеется в виду скачкообразное изменение этих величин при изменении температуры, давления и т. п., а не скачкообразное изменение во времени (насчёт последнего см. ниже раздел Динамика фазовых переходов). Наиболее распространённые примеры фазовых переходов первого рода: плавление и затвердевание, кипение и конденсация, сублимация и десублимация На фазовой диаграмме вещества различные термодинамические фазы занимают определённые области. Линии, разделяющие различные термодинамические фазы, называются линиями фазового перехода. Если вещество находится в условиях, отвечающих точке внутри какой-либо области, то оно полностью находится в этой термодинамической фазе. Если же состояние вещества отвечает точке на одной из линий фазовых переходов, то вещество в термодинамическом равновесии может находиться частично в одной, а частично в другой фазе. Пропорция двух фаз определяется, как правило, полной энергией, запасённой системой.

31

первый закон термодинамики

Первый закон термодинамики является обобщением закона сохранения и превращения энергии для термодинамической системы. Он формулируется следующим образом:

Изменение ΔU внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A, совершенной системой над внешними телами.

ΔU = Q – A.

Первый закон термодинамики является обобщением опытных фактов. Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую. Важным следствием первого закона термодинамики является утверждение о невозможности создания машины, способной совершать полезную работу без потребления энергии извне и без каких-либо изменений внутри самой машины. Такая гипотетическая машина получила название вечного двигателя первого рода.

32

Энтропия второй закон термодинамики.

Энтропия ( поворот, превращение) — понятие, впервые введённое Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального.

Второй Закон Термодинамики, как и Первый (Закон сохранения энергии) установлен эмпирическим путем. Впервые его сформулировал Клаузиус: "теплота сама собой переходит лишь от тела с большей температурой к телу с меньшей температурой и не может самопроизвольно переходить в обратном направлении".

Рассмотрим систему из двух контактирующих тел с разными температурами. Тепло пойдет от тела с большей температурой к телу с меньшей, до тех пор, пока температуры обоих тел не выровняются

33

Изопроцессы и их описание

Макропараметры: давление, объем и температура описывают состояние газа. Если при неизменна массе газа один из параметров не изменяется, получим изопроцессы Изобарный процесс.

P=const, V/T=const

V=const*T –прямо пропорциональная зависимость. График - линейный

Изохорный процесс.

V=const, p/T=const

P=const*T – прямо пропорциональная зависимость. График - линейный

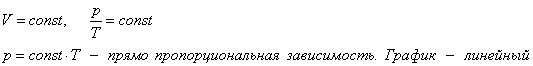Изотермический процесс.

T=const, pV=const

P=const*1/V – обратно пропорциональная зависимость. График – гипербола.

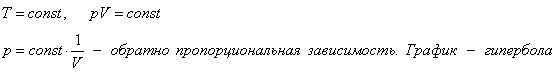Изопроцессы - это процессы, протекающие при неизменном значении одного из макроскопических параметров (р, V, Т).