2.2.2 Момент импульса. Момент инерции материальной точки..
Поскольку вращательное движение любого объемного тела можно представить как движение материальных точек, его составляющих, по окружностям разного радиуса, достаточно рассмотреть движение одной материальной точки массой m по окружности произвольного радиуса r относительно некоторой оси вращения ОО′ с некоторой скоростью V.
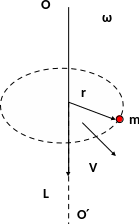
Для описания любой вращающейся материальной точки можно ввести физическую величину, называемую моментом импульса и определяемую векторным произведением радиус-вектора на вектор импульса:
L = [r ×p] |
(2.2.7) |
Поскольку угол между радиус-вектором и вектором скорости, направленным по касательной к окружности в данной точке, всегда 900, получаем величину момента импульса:
L = r p = r m V |
(2.2.8) |
Используя связь между линейной и угловой скоростями (1.3.5) V = r ω,
получаем определение момента импульса через угловые параметры:
L = r p = m r 2ω = I ω |
(2.2.9) |
где I = m r 2 –момент инерции материальной точки, являющийся мерой ее инертности при вращательном движении.
2.2.3. Момент инерции тела вращения.
Если требуется определить момент инерции тела вращения, то необходимо просуммировать непрерывно все материальные точки его составляющие, каждая из которых обладает элементарным моментом инерции:
dI = dm r 2 |
(2.2.10) |
Тогда
Iтела=∫dI = ∫dm r 2 |
(2.2.11) |
Пример.
Определим момент инерции диска радиусом R и высотой h, изготовленного из материала плотностью ρ, относительно собственной оси, проходящей через его центр ОО′:
Для этого воспользуемся симметрией диска и мысленно разобьем диск на бесконечно большое число бесконечно тонких кольцевых поверхностей внутренним радиусом r ,толщиной dr и высотой h.
Тогда,
Iоо′=∫dI = ∫ r 2dm =∫ r 2ρdVк = ∫ r2ρh2πrdr =
= 2πhρ 0∫R r3 dr =2πhρR4/4 =mдискаR2/2 |
(2.2.12) |
где масса диска mдиска = ρVдиска = ρ πR2 h
Аналогично можно рассчитать момент инерции однородного шара:
I = 2mшараR2/5.
8. Уравнение моментов. Основное уравнение динамики вращательного движения.
Анализируя различные примеры вращательного движения, можно сделать вывод о том, что под действием приложенных к телу внешних сил его момент импульса измениться. Поэтому можно утверждать, что результирующий момент внешних сил, действующих на тело, приводит к изменению момента импульса с течением времени. Другими словами, момент силы характеризует быстроту изменения момента импульса тела. Это утверждение представляет собой уравнение моментов, которое можно записать так:
M = dL/dt |
(2.2.15) |
Где: M=∑ Mi - сумма моментов внешних сил.
Используя определение момента импульса через угловые параметры (2.2.9), определение углового ускорения (1.2.4) и считая, что момент инерции тел не изменяется с течением времени, получаем основное уравнение динамики вращательного движения:
M = d(Iω)/dt = I dω/dt = Iβ |
(2.2.16) |
Это уравнение представляет собой аналог второго закона Ньютона для случая вращательного движения.
20.
Потенциал и напряженность гравитационного поля
Гравитационное поле является потенциальным полем, для его описания удобно воспользоваться понятием гравитационного потенциала U, дифференциал которого dU по своему физическому смыслу является работой, затрачиваемой для перемещения материальной точки с единичной массой на расстояние dr в рассматриваемом гравитационном поле. Для сферического тела с равномерно распределенной массой потенциал гравитационного поля определяется следующим образом:
U = GM / r,
где M – масса Земли (притягивающего тела); G – универсальная гравитационная постоянная; r – расстояние от центра тела до заданной точки.
Напряжённость гравитацио́нного по́ля — векторная величина, характеризующая гравитационное поле в данной точке и численно равная отношению силы тяготения, действующей на тело, помещённое в данную точку поля, к гравитационной массе этого тела: напряжённость гравитационного поля численно (и по размерности) равна ускорению свободного падения в этом поле.
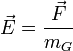
13.