6.Инерциальные и неинерциальные системы отсчета.
Выбирая систему отсчета, мы связываем ее с телом отсчета, на которое не накладываются никакие ограничения с точки зрения его движения.
Система отсчета, связанная с покоящимся или движущимся равномерно прямолинейно телом, называется инерциальной (ИСО).
Система отсчета, связанная с движущимся неравномерно телом, называется неинерциальной (НСО).
В неинерциальных системах отсчета, наравне с реальными силами тяжести, упругости и трения, возникают силы инерции, которые необходимо учитывать при записи законов Ньютона.
Сила инерции прямопропорциональна массе тела и противоположно направлена по отношению к вектору ускорения НСО:
Fи = – maнсо |
2.1.6 |
В неинерциальной системе отсчета, связанной с ускоренно движущимся лифтом, помимо уже известных сил, появляется сила инерции, противоположная ускорению лифта:
Ускорение тела относительно лифта отсутствует, поэтому в проекции на ось O′X′, получаем:
0 = mg – N – maнсо |
|
Ясно, что результаты обоих решений совпадут. Это подтверждает факт независимости конечного результата от выбора системы отсчета.
7. Динамическое описание вращательного движения.
2.2.1 Момент силы.
Начнем с простого примера: вы, входя в аудиторию, открыли дверь. Что заставило дверь вращаться относительно своей оси. Только ли из соображений удобства дверная ручка располагается вдали от оси вращения?
Для того чтобы ответить на эти вопросы, проведем эксперимент, прикладывая одну и ту же силу к двери на разном расстоянии от оси вращения. Вывод: чем ближе прилагается сила к оси вращения, тем сложнее открыть дверь. Это означает, что причиной вращательного движения служит не только сила, а параметр, зависящий еще и от расстояния, на котором эта сила приложена относительно оси вращения.
Векторная величина, определяемая векторным произведением радиус – вектора, проведенного от оси вращения в точку приложения силы, на саму действующую силу, называется моментом силы:
M = [r × F] |
(2.2.1) |
Направление момента силы определяется по правилу левой руки, четыре пальца которой направляются вдоль радиус-вектора так, чтобы вектор силы входил в ладонь. Тогда отогнутый под прямым углом большой палец укажет направление вектора момента силы:
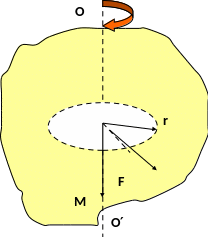
Величина момента силы определяется произведением силы на плечо l, которое представляет собой кратчайшее расстояние от оси вращения до линии действия силы. Опустив перпендикуляр на линию действия силы, получаем:
M = F l =F r sin α |
(2.2.2) |
где α – угол между радиус-вектором r и вектором силы F.
Аналогом первого закона Ньютона является условие равновесия, согласно которому тело находится в состоянии равновесия, если алгебраическая сумма моментов всех сил (с учетом их знаков), действующих на тело равна нулю. При этом моменты сил, вращающих тело против часовой стрелки принято считать положительными, вращающие тело по часовой стрелке – отрицательными:
Σ M = 0 |
(2.2.3) |
Например, применяя рычажные весы для взвешивания продуктов, мы используем условие равновесия, добиваясь того, чтобы вес взвешиваемого тела и вес гири создавали одинаковые по величине и противоположные по направлению моменты сил. Однако недобросовестные продавцы, изменяя положение груза (или гири) могут добиться создания того же вращательного момента меньшего по весу груза:
M1 – M2 = 0 |
(2.2.4) |
или
F1 R1 = F2 R2 |
(2.2.5) |
Поскольку F1=m1g, F2=m2g, получаем, что, сдвигая груз к краю весов, т.е. увеличивая расстояние от оси вращения до центра масс груза R1, и (или) сдвигая гирю к ближе к центру весов, т.е. уменьшая расстояние R2, возможно добиться меньшей, по сравнению с гирей, массы взвешиваемого тела при одинаковых вращательных моментах:
m1 R1 = m2 R2 |
(2.2.6) |