4. Криволинейное движение. Нормальное и тангенциальное ускорения.

Каждый участок криволинейной траектории одновременно можно рассматривать как отрезок, принадлежащий некоторой прямой, и дугу, лежащую на некоторой окружности, радиус которой R называют радиусом кривизны траектории в данной точке. Это означает, что для описания криволинейного движения можно использовать как линейные параметры, характеризующие поступательное движение, так и угловые параметры, описывающие вращательное движение, а также, что между линейными и угловыми параметрами существует определенная связь.

Нормальное и тангенциальное ускорения.

Рассмотрим в качестве криволинейной траектории окружность.

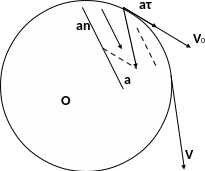
Вспомним определение линейного ускорения (1.6), в котором не указано, каким образом изменяется скорость тела. Очевидно, что в общем случае криволинейного движения скорость тела может изменяться как по величине, так и по направлению, поэтому здесь должны существовать два вида линейного ускорения:

• Тангенциальное, или касательное, ускорение a_τ, характеризующее изменение линейной скорости по величине;

• Нормальное, или центростремительное, ускорение a_n, характеризующее изменение скорости по направлению и существующее при любом, даже равномерном, криволинейном движении.

Полное линейное ускорение представляет собой векторную сумму указанных ускорений:

a = aτ + an

(3.1)

Величину можно определить по теореме Пифагора:

_______ a = √ aτ2 + an2

(3.2)

5. Динамическое описание поступательного движения.

2.1.1. Импульс тела. Сила.

Рассмотрим небольшой эксперимент, заключающийся во взаимодействии между двумя телами. Например, вы пытаетесь поймать рукой теннисный мячик и футбольный мяч, движущиеся с одинаковой скоростью V. Очевидно, что футбольный мяч, имеющий большую массу, поймать сложнее, так как его импульс при той же скорости окажется больше. Импульс является мерой количества движения тела и представляет собой векторную величину, численно равную произведению массы тела на его скорость.

p = m V, [кг·м/с]

2.1.1

Здесь в качестве характеристики тела, впервые появляется масса m [кг], являющаяся мерой его инертных свойств. Свойства тела, характеризующие его способность сохранять состояние предшествующего движения, называются инертностью.

Мерой воздействия одного тела на другое служит сила, характеризующая быстроту изменения импульса тела и определяемая отношением бесконечно малого его изменения к интервалу времени, за который это изменение произошло:

F = dp/dt, [Ньютон = Н]

2.1.2

2.1.2. Законы Ньютона.

Интуитивно силу можно определить как любой вид тол­чка или натяжения. Когда вы толкаете перед собой тележку с продуктами, вы действуете на нее с некоторой силой. Дети, тянущие игрушечную тележку, также прила­гают к ней силу. Когда двигатель поднимает лифт, или молоток бьет по гвоздю, или ветер дует на листья дерева - во всех этих случаях действует сила. Мы говорим, что тела падают потому, что на них действует сила тяжести. Силы не всегда вызывают движение. Например, можно очень энергично толкать тяжелый стол или холо­дильник, а предметы при этом могут не сдвинуться.

Великая теория движения принадлежит Ньютону. Ньютоновский анализ движения обоб­щен в его «трех законах движения». В своих знаменитых «Математических началах натуральной философии», ко­торые были опубликованы в 1687 г. и содержали почти все его труды по вопросам движения, Ньютон прямо заявил о своей признательности Галилею.

Галилей утверждал, что для тела столь же естественно совершать горизонтальное движение с посто­янной скоростью, как и пребывать в состоянии покоя. Чтобы понять точку зрения Галилея, понаблюдаем за движением в горизонтальной плоскости, в котором не участвует сила тяжести. Чтобы толкать с постоянной скоростью по плоскости стола предмет, имеющий шеро­ховатую поверхность, требуется некоторое усилие. Одна­ко, чтобы толкать с той же скоростью предмет той же массы, но по столу с очень гладкой поверхностью, потре­буется меньшая сила. Наконец, если между поверхностя­ми предмета и стола поместить слой масла или какой-ни­будь другой смазки, то для передвижения предмета не потребуется почти никаких усилий. (Эти наблюдения вполне могут показаться вам совершенно очевидными; в противном случае вы можете сами проделать эти неслож­ные эксперименты.) Заметим, что в каждом из примеров сила, необходимая для поддержания движения, станови­лась все меньше и меньше. Следующий шаг заключается в обобщении этих фактов на случай, когда предмет совсем не испытывает трения о поверхность стола (или между ними имеется идеальная смазка). Теоретически можно себе представить, что, если однажды привести предмет в состояние движения, он будет двигаться по столу с посто­янной скоростью без приложения какой-либо силы. Си­туацию, очень близкую к описанной, можно наблюдать, когда стальной шарик из подшипника катится по твердой горизонтальной поверхности.

Потребовался гений Галилея, чтобы вообразить идеа­лизированный мир (в данном случае - мир без трения) и осознать, что он может привести к более продуктивному взгляду на реальный мир. Именно эта идеализация приве­ла Галилея к замечательному выводу о том, что если на предмет не действует никакая сила, то он будет продол­жать двигаться по прямой с постоянной скоростью. Пред­мет станет двигаться медленнее только в том случае, когда на него действует сила. Таким образом, Галилей рассматривал трение как силу, родственную обычным толчкам и натяжениям.

Действительно, первый закон Ньютона очень близок к выводам Галилея. Он гласит: всякое тело сохраняет состояние покоя или равномерного и прямолинейного движения до тех пор, пока действующие на него силы не выведут его из этого состояния.

Стремление тела сохранять состояние покоя или рав­номерного прямолинейного движения называется инерт­ностью. В силу этого первый закон Ньютона часто назы­вают законом движения по инерции.

Первый закон Ньютона утверждает, что если на тело не действует результирующая сила, т.е. действие всех сил скомпенсировано, то оно продолжает пребывать в состо­янии покоя, а если тело движется, то оно продолжает движение по прямой с постоянной скоростью:

Σ F = 0

2.1.3

Но что происходит, если на тело, все-таки, действует сила? Нью­тон понимал, что скорость тела изменится. Результи­рующая сила, или равнодействующая всех сил, приложен­ных к телу, может увеличить скорость тела. Если сила направлена против направления движения тела, то она уменьшит его скорость. Если равнодействующая сил нап­равлена под углом к направлению движения тела, то и величина, и направление скорости тела будут меняться. Таким образом, равнодействующая всех сил, приложенных к телу, приводит к ускорению.

Второй закон Ньютона утверждает, что ускорение тела пропорционально действующей на тело результирующей силе и обратно пропорционально его массе. Результирующая сила равна векторной сумме всех дейст­вующих на тело сил:

a = Σ F /m

2.1.4

Согласно второму закону Ньютона результирующая сила является причиной поступательного движения тела, поэтому его называют основным законом поступательного движения.

Возникает естественный вопрос о том, откуда появляются силы? Наблюдения наводят на мысль, что сила, приложенная к любому телу, возникает в результате воздействия другого тела. Лошадь тянет повозку, человек толкает тележку с продуктами, молоток бьет по гвоздю, магнит притягивает железную иглу. В каждом из этих случаев одно тело (например, молоток) действует на другое (например, гвоздь) с опре­деленной силой и второе тело испытывает воздействие этой силы. Однако Ньютон осознал, что ситуация не может быть столь односторонней. Действительно, хотя молоток действует на гвоздь, гвоздь в свою очередь тоже действует на молоток, потому что скорость молотка при контакте с гвоздем быстро уменьшается до нуля. Только весьма значительная сила может вызвать такое быстрое торможение. Поэтому Ньютон пришел к выводу, что оба тела нужно рассматривать на общих основаниях. Молоток действует на гвоздь, но и гвоздь в ответ тоже действует на молоток.

В этом и состоит третий закон Ньютона: всякий раз, когда одно тело действует с некоторой силой на другое, со стороны второго тела на первое действует сила противодействия, равная по величине и противоположная по направлению силе действия:

F 1→2= –F 2→1

2.1.5

Иногда этот закон сокращенно формулируют так: «Сила действия равна по величине и противоположна по направлению силе противодействия». Чтобы избежать путаницы, важно помнить, что силы «действия» и «про­тиводействия» приложены к различным телам.