1. Системы отсчета.

Все события происходят в определенном месте пространства в данный момент времени. Чтобы задать положение тела в пространстве, достаточно трех координат. Ещё одно число задает момент времени.

Говорят, что пространство, в котором мы живем, трехмерно. Чтобы понять это утверждение, рассмотрим пространство с другим количеством измерений. Представьте себе линию, не имеющую толщины. На такой линии могут разместиться материальные точки и отрезки. Чтобы задать их положение достаточно одного измерения /координаты “x”/ -это одномерное пространство. Два объекта в таком пространстве не смогли бы обойти друг друга, т.к. здесь существует всего одно измерение и отсутствует понятие ширины.

Но стоит нашу линию развернуть в плоскость, не обладающую толщиной, как мы получим двухмерное пространство. В нем смогут жить плоские амебы, кляксы и рисованные человечки, которые при встрече друг с другом вынуждены перепрыгивать через голову. В этом случае существует всего два измерения /координаты “x” и ”y”/.

Для нормального существования человека и всего окружающего мира необходимо ещё одно третье измерение /координаты “z”/. Получим некоторый трехмерный ящик, в котором мы можем достаточно уютно жить.

Сила нашего воображения дополняет наш трехмерный мир четвертым измерением - временем. Строго говоря, наше пространство – время четырехмерно, но время течет равномерно в одном направлении и его невозможно повернуть вспять, поэтому временное измерение трудно представить.

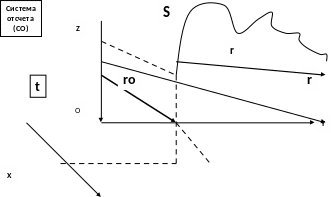
Чтобы задать положение тела в данный момент времени в пространстве, необходимо ввести понятие системы отсчета.

Система отсчета - это совокупноcть тела отсчета /0/, связанных с ним осей координат /x, y, z/ и способа измерения.

Изобразить систему отсчета /СО/ можно с помощью правой тройки векторов /если левая рука направлена по оси “x”, а ось “y” входит в ладонь, то отогнутый под прямым углом большой палец укажет направление оси “z”/.

Чтобы задать положение материальной точки относительно произвольно выбранного тела отсчета, необходимо провести из точки О радиус- вектор в точку, где в данный момент времени находится тело. Радиус- вектор, как луч света, высвечивает положение тела относительно тела отсчета. Он определяет положение тела и имеет три проекции на оси координат:

r (x, y, z), [метр = м]

(1.1)

Эти проекции являются координатами точки, где в данный момент времени находится тело.

Радиус- вектор изменяется с течением времени и любое движение можно описать функцией r(t). А так же системой трех скалярных функций:

x (t), y (t), z (t).

2. Равномерное поступательное движение.

Перемещение r [метр = м] представляет собой направленный отрезок, проведенный из начального в конечное положение тела в пространстве, длина которого есть кратчайшее расстояние между этими точками.

Линия, которую описало тело при своем движении, называется траекторией.

Длина траектории есть пройденный телом путь S.

Для описания любого движения требуется определить понятие скорости, как быстроту изменения положения тела в пространстве.

Чтобы узнать скорость тела в данный момент времени (мгновенную скорость), необходимо все перемещение тела r разделить мысленно на бесконечно малые участки dr, на каждом из которых скорость можно считать неизменной. Тогда мгновенную скорость можно определить как отношение бесконечно малого перемещения к интервалу времени, за который это перемещение произошло:

V = dr/dt, [метр/секунда = м/с]

(1.2)

Мгновенное перемещение тела совпадает с направлением его мгновенной скорости. Если же требуется найти конечное перемещение тела, необходимо просуммировать непрерывно все бесконечно малые перемещения, т.е. следует произвести интегрирование от начального t_o до конечного момента времени t:

r = r – ro = ∫ Vdt

(1.3)

Если тело за любые равные промежутки времени совершает равные перемещения, то его движение является равномерным. В этом случае результат интегрирования очень прост:

r = ro + V(t -to)

(1.4)

Считая, что начальный момент времени равен нулю /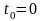 /, можно записать систему скалярных уравнений, позволяющих определить координаты тела в любой момент времени равномерного поступательного движения:

x = xo + Vx (t - to); y = yo + Vy (t - to); z = zo + Vz (t - to)

(1.5)