8. Туннельный эффект. Вероятность прохождения частицы через барьер.

   Туннельный эффект (туннелирование) – прохождение частицы (или системы) сквозь область пространства, пребывание в которой запрещено классической механикой. Наиболее известный пример такого процесса – прохождение частицы сквозь потенциальный барьер, когда её энергия Е меньше высоты барьера U₀. В классической физике частица не может оказаться в области такого барьера и тем более пройти сквозь неё, так как это нарушает закон сохранения энергии. Однако в квантовой физике ситуация принципиально другая. Квантовая частица не движется по какой-либо определенной траектории. Поэтому можно лишь говорить о вероятности нахождения частицы в определенной области пространства ΔрΔх > ћ. При этом ни потенциальная, ни кинетическая энергии не имеют определенных значений в соответствии с принципом неопределенности. Допускается отклонение от классической энергии Е на величину ΔЕв течение интервалов времени  t, даваемых соотношением неопределённостейΔЕΔt > ћ (ћ = h/2π, где h – постоянная Планка).

      Возможность прохождения частицы сквозь потенциальный барьер обусловлена требованием непрерывной волновой функции на стенках потенциального барьера. Вероятность обнаружения частицы справа и слева связаны между собой соотношением, зависящим от разности E - U(x) в области потенциального барьера и от ширины барьера x₁ - x₂ при данной энергии.

    С увеличением высоты и ширины барьера вероятность туннельного эффекта экспоненциально спадает. Вероятность туннельного эффекта также быстро убывает с увеличением массы частицы.     Проникновение сквозь барьер носит вероятностный характер. Частица с Е < U₀, натолкнувшись на барьер, может либо пройти сквозь него, либо отразиться. Суммарная вероятность этих двух возможностей равна 1. Если на барьер падает поток частиц с Е < U₀, то часть этого потока будет просачиваться сквозь барьер, а часть – отражаться. Туннельное прохождение частицы через потенциальный барьер лежит в основе многих явлений ядерной и атомной физики: альфа-распад, холодная эмиссия электронов из металлов, явления в контактном слое двух полупроводников и т.д.

9 Квантовый осциллятор. Энергетический спектр и правила отбора.

Аннотация: изучение качественной стороны решения уравнения Шредингера для гармонического осциллятора, выяснение отличий получаемых результатов от выводов классической механики. (Традиционное изложение темы, дополненное демонстрациями на компьютерных моделях.)

Содержание

Одна из важных задач о движении микрочастиц – это задача о движении гармонического осциллятора - системе, способной совершать гармонические колебания.История квантовой теории реально начинается с Макса Планка, который в 1900 г. получил формулу для правильного описания спектрального распределения теплового излучения. Планк пришел к выводу, что не может обеспечить вывод своей магической формулы для распределения излучения, если только не сделать предположения, которое с философской точки зрения он считал почти неприемлемым. Это предположение заключалось в том, что рассматриваемые им в качестве излучателей гармонические осцилляторы должны обладать энергиями, не распределенными как непрерывные переменные (чего следовало бы ожидать), а принимающими дискретные и регулярным образом расположенные значения. Осцилляторы с частотой υ должны были обладать значениями энергии, которые были бы кратны, т.е. n раз умножены (где n = 0,1, 2,3,...) на нечто, названное им квантом энергии hυ.

Рассмотрим одномерный случай. (Трехмерные задачи сложны в математическом отношении, а практически все принципиальные особенности движения микрочастиц можно выявить и на одномерных задачах.) Изменение потенциальной энергии по оси x описывается формулой

Какие примеры движения окружающего мира хотя бы приближенно описываются такой потенциальной функцией?

• Колебания маятника с малой амплитудой.

• Другой пример – вертикальные колебания грузика, подвешенного на пружине.

В мире микрочастиц примерами могут быть колебания двухатомной молекулы или колебания атомов в кристаллах. Существенным для всех примеров является ограничение движения некоторой областью значений x. Частица не может покинуть параболическую потенциальную яму, края которой уходят на бесконечность.

Из классической механики известно, что проекция движения частицы на ось x представляет собой синусоидальное колебание около положения равновесия x = 0 с частотой:

Точки a₀ и -a₀, в которых полная энергия частицы E равна потенциальной энергии, являются для частицы точками поворота. Плотность вероятности обнаружения колеблющейся частицы в различных точках оси x описывается формулой

Минимальна вероятность найти частицу около положения равновесия, где она движется с максимальной скоростью. Вблизи точек поворота частица как бы "зависает", и там вероятность обнаружения максимальна.

Оценка минимальной энергии осциллятора

Посмотрим, к каким выводам о характере движения приводит квантовая механика. Начнем с простой оценки минимального значения энергии осциллятора E. Полная энергия осциллятора E складывается из кинетической и потенциальной энергий:

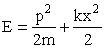
Используя соотношение неопределенности Гейзенберга, в качестве оценки значения импульса p возьмем p ~ ћ/x.

Для малых значений x кинетическая энергия превышает потенциальную, тогда как при больших значениях x имеет место обратное соотношение между ними. Для основного состояния, где энергия минимальна, найдем минимум функции (2). Значение переменной x_min, соответствующее минимуму, равно:

а соответствующее значение энергии E имеет порядок

Заметим, что оценка энергии основного состояния дает ненулевое(!) значение. Уже простые вычисления приводят к нетривиальному результату.

Еще одной важной особенностью спектра (4.81) является наличие так называемых нулевых колебаний - колебаний с энергией , соответствующих значению квантового числа. Отличие от нуля минимальной энергии осциллятора характерно, как мы уже видели, для всех квантовых систем и является следствием соотношения неопределенностей. В реальных квантовых системах, например, кристаллах, эти колебания сохраняются, как показывает опыт, даже при температурах, близких к абсолютному нулю, когда, казалось бы, все тепловое движение должно прекратиться.

Нулевые колебания играют в физике весьма важную роль, в частности они обусловливают отсутствие кристаллизации жидкого гелия при нормальном давлении даже при абсолютном нуле температур. Велика роль нулевых колебаний и в объяснении природы сил молекулярных взаимодействий, физических особенностей поверхностного натяжения, адсорбции и других молекулярных явлений. На эксперименте наличие нулевых колебаний наблюдается, в частности, в опытах по рассеянию света кристаллами при низких температурах.

Формула 4.82 (4.82)

Условия, которые определяют изменение квантовых чисел при разрешенных переходах системы из одного состояния в другое, называются правилами отбора. Таким образом, правила отбора, характеризующие испускание и поглощение электромагнитного излучения гармоническим осциллятором, имеют вид (4.82) .