Функции нескольких переменных.

1.Основные понятия.

Определение. Если каждой паре (x,y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.

Обычно функция нескольких переменных задается явным аналитическим способом. Например: z=3x+5y²,u=xy+z² и т.д.

Встречается также и неявное задание таких функций, например: z-2x-sinxy=0.

 Упорядоченная пара чисел (x,y) может рассматриваться как точка на плоскости, т.е. Z есть функция точки (x,y).

Чтобы задать функцию z=f(x,y), надо не только указать правило нахождения z по заданным x и y, но и то множество (называемое областью задания функции) пар значений, которые могут принимать аргументы x и y.

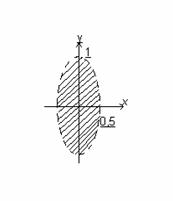
Например, функция z= задана только при 1-y >0, т.е. внутри эллипса y²+4x²<1 с полуосями, а=0,5 и в=1 не включая точки, лежащие на эллипсе.

 

Определение. Если каждой совокупности значений переменных x,y,z…t соответствует определенное значение переменной w, то w называется функцией независимых переменных x,y,z…t и записывается w=f(x,y,z…t).

Для функции трех переменных областью определения является упорядоченная тройка чисел (x,y,z), т.е. некоторая совокупность точек пространства. Область определения функции четырех и большего числа переменных не допускает простого геометрического истолкования.

Функции двух переменных допускают графическую иллюстрацию. Графиком функции z=f(x,y), заданной на некотором множестве D точек плоскости ХОУ, называется множество точек (x,y,z) пространства, у которых (x,y) принадлежит D, а z=f(x,y). В наиболее простых случаях такой график представляет собой некоторую поверхность.

Например, графиком функции z=4-x²-y² является параболоид.

 

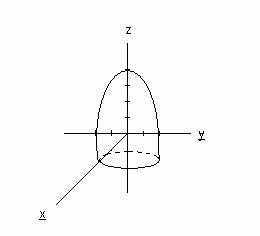
Функции трех и большего числа переменных не имеют геометрического представления.

            2.Непрерывность функции нескольких переменных.

Определение. Число А называется пределом функции f(M), где М(x₁,x₂,…x_n) – точка n-мерного пространства, при стремлении точки М к точке М₀(x₁⁰,x₂⁰,…x_n⁰) любым образом, если для всякого сколь угодно малого  >0 существует такое число  >0, что из условия  < , где  - расстояние между точками М и М₀, следует  < .

Обозначается:

А  .

Пусть z=f(x,y). Придадим x и y приращения  и  . Получим приращение   функции z=f(x,y). Если

                         ,                                                                                   (1)

 т.е. бесконечно малым аргументам соответствует бесконечно малое приращение функции, то говорят, что функция непрерывна.

Распишем  x₀+ y+ -f(x₀,y₀) и положим x₀₊ x=x,y₀+  ,то выражение(1) можно записать в виде

                         f(x,y)=f(x ₀,y₀),                                                                      (2)

т.е. непрерывность функции означает, что ее предел равен ее значению от пределов аргументов.

 Функция, непрерывная в каждой точке некоторой области, называется непрерывной в области. Если в некоторой точке не выполняется условие (2), то эта точка называется точкой разрыва.