
- •Предмет статика. Основные понятия статики.
- •Сила. Система сил. Силы сосредоточенные и распределенные.
- •Аксиомы статики и их следствия.
- •16.Трение скольжения. Равновесие при наличии трения скольжения.
- •17.Трение качения. Равновесие при наличии трения качения.
- •2Проекция зависит только от скорости Для остальных координат все тоже самое только вместо х у или z
- •2 Закон Ньютона.
- •47. Постановка задачи о движении несвободной материальной точки, системы материальных точек. Связи. Классификация связей.
- •50. Принцип возможных перемещений.
- •51. Обобщенные координаты. Обобщенные силы.
- •52. Принцип Даламбера и Даламбера-Лагранжа.
16.Трение скольжения. Равновесие при наличии трения скольжения.
 Закон
Амонтона Кулона
Если
два тела I и II взаимодействуют друг с
другом, соприкасаясь в точке А, то всегда
реакцию RA,
действующую, например, со стороны тела
II и приложенную к телу I, можно разложить
на две составляющие: NA
направленную по общей нормали к
поверхности соприкасающихся тел в точке
А, и ТА,
лежащую в касательной плоскости.
Составляющая NA
называется
нормальной реакцией, сила ТА называется
силой трения скольжения — она препятствует
скольжению тела I по телу II. В соответствии
3 зак-ом Ньютона на тело II со стороны
тела I действует равная по модулю и
противоположно направленная сила
реакции. Угол j между
Закон
Амонтона Кулона
Если
два тела I и II взаимодействуют друг с
другом, соприкасаясь в точке А, то всегда
реакцию RA,
действующую, например, со стороны тела
II и приложенную к телу I, можно разложить
на две составляющие: NA
направленную по общей нормали к
поверхности соприкасающихся тел в точке
А, и ТА,
лежащую в касательной плоскости.
Составляющая NA
называется
нормальной реакцией, сила ТА называется
силой трения скольжения — она препятствует
скольжению тела I по телу II. В соответствии
3 зак-ом Ньютона на тело II со стороны
тела I действует равная по модулю и
противоположно направленная сила
реакции. Угол j между
предельной реакцией R и нормалью к поверхности называется углом трения. tgj=Tmax/N=f.
17.Трение качения. Равновесие при наличии трения качения.
РИСУНОК.
Силу
трения качения нельзя учитывать тела
абсолютно
твердые.
РИСУНОК.




 Сопротивление,
возникающее при качении одного тела по
другому, называется трением качения.
Оно обусловлено деформациями этих тел
.На рисунке 28 показано два разных
состояния одного и того же катка. Слева
изображен каток в состоянии покоя.
Удельное давление на контактной площадке
(которая образуется в результате
деформации контактирующих звеньев)
распределяется симметрично (по теории
Герца – по эллиптическому закону)
относительно линии действия приложенной
нагрузки. В результате нормальная
реакция совпадает с линией действия
внешней силы и уравновешивает ее.Справа
каток движется под действием силы F,
приложенной к катку на некотором плече
h. Происходит перераспределение деформации
таким образом, что впереди катка (по
ходу движения) образуется волна
деформации. Эпюра удельного давления
трансформируется и нормальная реакция
смещается вперед по ходу движения катка
на величину k, создавая момент сопротивления.
Этот момент сопротивления называется
моментом трения качения, плечо k –
коэффициентом трения качения. Формула
для определения момента трения качения
аналогична формуле для определения
силы трения в поступательной паре
(коэффициент трения качения, как и
коэффициент трения скольжения, является
справочным материалом – определяется
экспериментально). Однако надо помнить,
что коэффициент трения качения величина
размерная – имеет линейную размерность
(м, см, мм). В высшей кинематической паре
возможно не только качение одного звена
по поверхности другого, но и относительное
скольжение соприкасающихся поверхностей.
Поэтому представляет интерес условие,
при котором будет происходить тот или
иной процесс. Для того чтобы звено
катилось, движущий момент должен быть
больше момента сопротивления (или равен
ему). В данном случае в качестве момента
сопротивления выступает момент трения
качения: Для того чтобы звено скользило
вдоль поверхности второго, движущая
сила должна быть больше силы трения
скольжения (или равна ей): Звено будет
двигаться по пути наименьшего
сопротивления. Поэтому будет происходить
чистое качение, если: Соответственно
условие чистого скольжения:При k/h = f
происходит неопределенное движение
(одновременное качение со скольжением).
Если движущая сила приложена в центре
катка, то вместо плеча h надо подставить
радиус катка r. Видно, что с уменьшением
радиуса резко возрастает сопротивление
качению и, с большей вероятностью, под
действием движущей силы каток будет
скользить (поэтому колеса транспортных
машин, требующих значительной проходимости
в любую погоду, – колесные трактора,
вездеходы, «внедорожники» – имеют
большой диаметр).Трением качения
называется сопротивление, возникающее
при качении одного тела по поверхности
другого.
Вследствие деформации тел
их касание происходит вдоль площадки
AB, появляется распределенная система
сил реакций, которая, согласно основной
теореме статики, может быть заменена
силой и парой (рисунок 2.18). Сила
раскладывается на две составляющие –
нормальную N и силу трения Fmp; пара сил
называется моментом сопротивления
качению MC.При равновесии тела момент
сопротивления качению определяется из
условий равновесия системы сил. При
этом установлено, что момент сопротивления
принимает значения от нуля до максимального
значения. Максимальное значение момента
сопротивления, соответствующее началу
качения, определяется равенством
MC
max=δN [Нм],
где δ – коэффициент трения
качения, измеряемый в метрах и зависящий
от материала контактирующих тел и
геометрии зоны контакта.
Сопротивление,
возникающее при качении одного тела по
другому, называется трением качения.
Оно обусловлено деформациями этих тел
.На рисунке 28 показано два разных
состояния одного и того же катка. Слева
изображен каток в состоянии покоя.
Удельное давление на контактной площадке
(которая образуется в результате
деформации контактирующих звеньев)
распределяется симметрично (по теории
Герца – по эллиптическому закону)
относительно линии действия приложенной
нагрузки. В результате нормальная
реакция совпадает с линией действия
внешней силы и уравновешивает ее.Справа
каток движется под действием силы F,
приложенной к катку на некотором плече
h. Происходит перераспределение деформации
таким образом, что впереди катка (по
ходу движения) образуется волна
деформации. Эпюра удельного давления
трансформируется и нормальная реакция
смещается вперед по ходу движения катка
на величину k, создавая момент сопротивления.
Этот момент сопротивления называется
моментом трения качения, плечо k –
коэффициентом трения качения. Формула
для определения момента трения качения
аналогична формуле для определения
силы трения в поступательной паре
(коэффициент трения качения, как и
коэффициент трения скольжения, является
справочным материалом – определяется
экспериментально). Однако надо помнить,
что коэффициент трения качения величина
размерная – имеет линейную размерность
(м, см, мм). В высшей кинематической паре
возможно не только качение одного звена
по поверхности другого, но и относительное
скольжение соприкасающихся поверхностей.
Поэтому представляет интерес условие,
при котором будет происходить тот или
иной процесс. Для того чтобы звено
катилось, движущий момент должен быть
больше момента сопротивления (или равен
ему). В данном случае в качестве момента
сопротивления выступает момент трения
качения: Для того чтобы звено скользило
вдоль поверхности второго, движущая
сила должна быть больше силы трения
скольжения (или равна ей): Звено будет
двигаться по пути наименьшего
сопротивления. Поэтому будет происходить
чистое качение, если: Соответственно
условие чистого скольжения:При k/h = f
происходит неопределенное движение
(одновременное качение со скольжением).
Если движущая сила приложена в центре
катка, то вместо плеча h надо подставить
радиус катка r. Видно, что с уменьшением
радиуса резко возрастает сопротивление
качению и, с большей вероятностью, под
действием движущей силы каток будет
скользить (поэтому колеса транспортных
машин, требующих значительной проходимости
в любую погоду, – колесные трактора,
вездеходы, «внедорожники» – имеют
большой диаметр).Трением качения
называется сопротивление, возникающее
при качении одного тела по поверхности
другого.
Вследствие деформации тел
их касание происходит вдоль площадки
AB, появляется распределенная система
сил реакций, которая, согласно основной
теореме статики, может быть заменена
силой и парой (рисунок 2.18). Сила
раскладывается на две составляющие –
нормальную N и силу трения Fmp; пара сил
называется моментом сопротивления
качению MC.При равновесии тела момент
сопротивления качению определяется из
условий равновесия системы сил. При
этом установлено, что момент сопротивления
принимает значения от нуля до максимального
значения. Максимальное значение момента
сопротивления, соответствующее началу
качения, определяется равенством
MC
max=δN [Нм],
где δ – коэффициент трения
качения, измеряемый в метрах и зависящий
от материала контактирующих тел и
геометрии зоны контакта.
18. Введение в кинематику. Основные понятия и объекты кинематики. [Механическое движение. Системы отчета.] Кинематика изучает движение объектов кинематики без учета причин вызывающих это движение – т.е. без учета сил. Объекты кинематики: 1. Материальная точка ; 2. Система материальных точек ;3. Абсолютно твердое тело 4. Система абсолютно твердых тел Материальная точка – это физическое тело размерами которого можно пренебречь, по сравнению с размерами области движения; Система материальных точек – совокупность материальных точек, которые каким либо образом обособленны от других материальных точек и других тел. Абсолютно твердое тело- физическое тело, размеры и формы которого остаются неизменными, тела не деформируемые. Система абсолютно твёрдых тел- совокупность абсолютно твёрдых тел, каким либо образом обособленных от других тел. Основные понятия кинематики являются: 1. Законы движения – зависимость координатных объектов, которые определяют его положение по времени. 2. Траектория – она применяется в случае материальной точки 3. Скорость – отношение пути ко времени 4. Ускорение – первая производная от скорости
19.Векторный
способ задания движения материальной
точки. Траектория. Скорость. Ускорение.
РИСУНОК. Геометрическое
место концов радиус-вектора называется
траекторией. Траектория – это годограф
радиуса вектора..
Траектория
– это геометрическое место точек
пространства, которая материальная
точка проходит в процесс движения.


 <a>=
<a>= Чтобы
иметь возможность определить параметры
движения точки необходимо задать закон
ее движения. В зависимости от известных
величин и поставленной задачи могут
быть использованы следующие способы
задания движения точки.
Векторный
способ задания движения точки
В этом
случае положение точки на плоскости
или в пространстве определяется
вектором-функцией( рис 1)Этот вектор
откладывается от неподвижной точки,
выбранной за начало отсчета, его конец
определяет положение движущейся
точки.Годограф r, т.е. положение концов
этого вектора в пространстве, определяет
траекторию движущейся точки. Ее скорость
в этом случае определяется как производная
от радиуса-вектора и направлена по
касательной к годографу r (по касательной
к траектории движения точки( рис 2,3)
Чтобы
иметь возможность определить параметры
движения точки необходимо задать закон
ее движения. В зависимости от известных
величин и поставленной задачи могут
быть использованы следующие способы
задания движения точки.
Векторный
способ задания движения точки
В этом
случае положение точки на плоскости
или в пространстве определяется
вектором-функцией( рис 1)Этот вектор
откладывается от неподвижной точки,
выбранной за начало отсчета, его конец
определяет положение движущейся
точки.Годограф r, т.е. положение концов
этого вектора в пространстве, определяет
траекторию движущейся точки. Ее скорость
в этом случае определяется как производная
от радиуса-вектора и направлена по
касательной к годографу r (по касательной
к траектории движения точки( рис 2,3)
Ускорение точки
(изменение ее скорости) определяется
как производная от скорости:
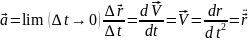 Вектор
ускорения направлен по касательной к
годографу вектора скорости (показано
на рис3)
20.Задание
движения методом декартовых координат.
Траектория. Скорость. Ускорение.
Вектор
ускорения направлен по касательной к
годографу вектора скорости (показано
на рис3)
20.Задание
движения методом декартовых координат.
Траектория. Скорость. Ускорение.
РИСУНОК.




 cos
cos cos
cos cos
cos V=
V=
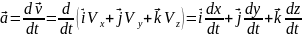



 a=
a= cos
cos cos
cos cos
cos
( ( ( 21.Задание движений методом полярных координат. Траектория. Скорость. Ускорение.))) РИСУНОК.
 =
=
 (t)
(t)
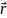 =
=

 =
=
 (t)
v=
(t)
v=
 _______
=
_______
=
 (
)
(
)
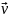 =
=
 =
= (
)=
(
)= +
+
 +
+
 =
=
 +
+
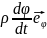
=
 +
+

 =
=

 =
=

22. Естественный трехгранник. Касательное и нормальное ускорения. Естественные оси (касательная, главная нормаль, бинормаль) – это оси подвижной прямоугольной системы координат с началом в движущейся точке. Их направление определяется траекторией движения.( рисунок) Касательная (с единичным вектором τ) направлена по касательной в положительном направлении отсчета дуговой координаты. Главная нормаль (n) направлена в сторону вогнутости траектории и образует вместе с касательной соприкасающуюся плоскость. Бинормаль (b) направлена перпендикулярно касательной и главной нормали так, что орты τ , n и b образуют правую систему координат. Главная нормаль и бинормаль образуют нормальную плоскость, бинормаль и касательная – спрямляющую. Координатные плоскости введенной подвижной системы координат (соприкасающаяся, нормальная и спрямляющая) образуют естественный трехгранник (натуральный триэдр), который перемещается вместе с движущейся точкой, как твердое тело. Его движение в пространстве определяется траекторией и законом изменения дуговой координаты.
23.Поступательное
движение абсолютно твердого
тела.
Поступательное движение – это
движение, при котором любая прямая,
связанная с телом, перемещается
параллельно самой себе. На рисунках 1 и
2 приведены примеры поступательного
движения: движение прямоугольника в
плоскости чертежа, движение каждой
кабины колеса обозрения.
Рисунок 3
Исходя из определения поступательного
движения, движение твердого тела может
быть задано в векторном виде формулой
(рисунок 2.2): rM=rA ⊕
AM. В этой формуле AM - вектор постоянный
по величине и направлению, поэтому
производная от него равна нулю. Для
скорости и ускорения произвольной точки
M получим:
![]() скорость
и ускорение произвольной точки. То есть
скорости и ускорения точек твердого
тела при поступательном движении равны
и одинаково направлены, а траектории
при наложении совпадают. Для определения
кинематических характеристик точек
тела достаточно знать закон движения
одной из них
24.
Вращение твердого тела вокруг закрепленной
оси.
скорость
и ускорение произвольной точки. То есть
скорости и ускорения точек твердого
тела при поступательном движении равны
и одинаково направлены, а траектории
при наложении совпадают. Для определения
кинематических характеристик точек
тела достаточно знать закон движения
одной из них
24.
Вращение твердого тела вокруг закрепленной
оси.
Вращением абсолютно твердого тела вокруг неподвижной оси называется движение при котором все точки лежащие на оси остаются неподвижны, а остальные движутся по окружности, центры которых лежат на оси, а плоскости кругов перпендикулярно оси. РИСУНОК.

 =
t +
=
t +
 t
t
 =
=
 +
+
 <
< >
=
>
=
 =
lim(
t ->0)
=
=
lim(
t ->0)
=
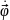
<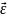 >=
>=
=
lim(
t->0)
=


РИСУНОК. Скорость вращения тела, определяющаяся приращением угла поворота тела за промежуток времени называется угловой скоростью. Быстрота изменения угла φ – это угловая скорость: Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны. Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном - противоположны. В технике угловая скорость часто задается в оборотах в минуту n[об/мин]. Один оборот – это 2π радиан: 25.Связь между линейными и угловыми величинами.
РИСУНОК.
 =R*
=R* ;
;
 =R
=R lim(
lim( )
=R
lim(
)
)
=R
lim(
)
v=Rw
= x
v=w
r sin
x
v=w
r sin =
w R
=
w R
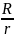 =
sin
=>R=r
sin
=
=
sin
=>R=r
sin
=
 x
x
 x
x

 =
x
=
x

 =
x
=
x

 =
x
=
x

 =
= =
(
x
)=
=
(
x
)=
 x
+
x
=
x
+
x
=
x
+
x
(
x
)
x
+
x
=
x
+
x
=
x
+
x
(
x
)
 =
x
( тангенсиальное ускорение)
=
x
( тангенсиальное ускорение)
 =
=
 R
R
 =
x
=
x
(
x
)
=
x
=
x
(
x
)
 =
=
 =
= =
= a=
a= tg
=
tg
=
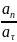 =
= =
=
26. Плоскопараллельное
движение твердого тела. Скорость.
Мгновенный центр скоростей.
Плоскопараллельным
движением абсолютно твердого тела
называется движение при котором можно
выбрать плоскость, и такую что все точки
твердого тела, лежащие на прямой
перпендикулярно к этой плоскости все
точки движутся одинаково.
РИСУНОК.
РИСУНОК.
РИСУНОК.


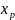 =
(t)
=
(t)
 =
(t)
- задано плоско- параллельное движение
абсолютно твердого тела
=
(t)
- задано плоско- параллельное движение
абсолютно твердого тела
= (t)
(t)
 - векторное задание
- векторное задание





 0=
0= => 0=
=> 0= 0=
0=
 w=
w=

 Теорема о проекции скоростей, двух
точек плоской фигуры на прямую их
соединяющую. Проекция скоростей точек
плоской фигуры на прямую их соединяющую
равны.
РИСУНОК.
Мгновенный
центр скоростей.
Мгновенный центр
скоростей называется точка, принадлежащая
плоской фигуре ( или не принадлежащая)
скорость которой равна 0, точка относительно
которой все точки фигуры в данный момент
времени совершают чисто вращательное
движение.
РИСУНОК.
AC=
Теорема о проекции скоростей, двух
точек плоской фигуры на прямую их
соединяющую. Проекция скоростей точек
плоской фигуры на прямую их соединяющую
равны.
РИСУНОК.
Мгновенный
центр скоростей.
Мгновенный центр
скоростей называется точка, принадлежащая
плоской фигуре ( или не принадлежащая)
скорость которой равна 0, точка относительно
которой все точки фигуры в данный момент
времени совершают чисто вращательное
движение.
РИСУНОК.
AC=


 27.Ускорение
при плоско параллельном движении.
27.Ускорение
при плоско параллельном движении.
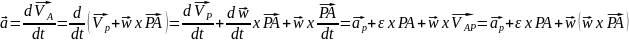



 РИСУНОК.
РИСУНОК.

tg
 28.
Сложное
движение материальной точки. Закон
сложения скоростей.
РИСУНОК.
Сложным
называют движение точки по отношению
к двум или нескольким системам
отсчета.
Движение той точки подвижной
системы отсчета, в которой в данный
момент находится движущаяся точка, по
отношению к неподвижной системе отсчета
называют переносным движением
k:
28.
Сложное
движение материальной точки. Закон
сложения скоростей.
РИСУНОК.
Сложным
называют движение точки по отношению
к двум или нескольким системам
отсчета.
Движение той точки подвижной
системы отсчета, в которой в данный
момент находится движущаяся точка, по
отношению к неподвижной системе отсчета
называют переносным движением
k:

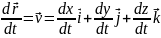



 k’:
k’:


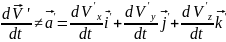 Закон
сложения скоростей.
Закон
сложения скоростей.



 a
r
e
a
r
e
 =
=


 -
скорость точки пространства k’,
где в данный момент находится материальная
точка обусловлена поступательным или
вращательным движением k’.
29.
Сложное движение материальной точки.
Закон сложения ускорений.
Сложным
называют движение точки по отношению
к двум или нескольким системам
отсчета.
Движение той точки подвижной
системы отсчета, в которой в данный
момент находится движущаяся точка, по
отношению к неподвижной системе отсчета
называют переносным движением
k:
k’:
Закон
сложения ускорений.
V=
-
скорость точки пространства k’,
где в данный момент находится материальная
точка обусловлена поступательным или
вращательным движением k’.
29.
Сложное движение материальной точки.
Закон сложения ускорений.
Сложным
называют движение точки по отношению
к двум или нескольким системам
отсчета.
Движение той точки подвижной
системы отсчета, в которой в данный
момент находится движущаяся точка, по
отношению к неподвижной системе отсчета
называют переносным движением
k:
k’:
Закон
сложения ускорений.
V=


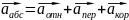 a
r
e
с
a
r
e
с
 =
=



 =
=

 =
=

 =
=

 =
= Переносное
ускорение – это ускорение точки
пространства системы k’,
где в данный момент находится материальная
точка обусловленное ускоренным
поступательным и вращательным движениями
k’.
РИСУНОК.
30.Введение
в динамику. Объекты и основные понятия
динамики. Сила. Масса.
Динамика
изучает движение объектов динамики с
учетом причин вызывающих изменения
движения, т.е. сил.
Объекты динамики:
1. Материальная
точка;2. Система материальных точек; 3.
Абсолютно твердое тело; 4. Система
абсолютно твердых тел
Материальная
точка – это
физическое тело размерами которого
можно пренебречь, по сравнению с размерами
области движения. Система
материальных точек
– совокупность материальных точек,
которые каким либо образом обособленны
от других материальных точек и других
тел. Абсолютно
твердое тело-
физическое тело, размеры и формы которого
остаются неизменными, тела не деформируемые.
Система
абсолютно твёрдых
тел- совокупность абсолютно твёрдых
тел, каким либо образом обособленных
от других тел.
Основные
понятия динамики являются:
1. Законы
движения –
зависимость координатных объектов,
которые определяют его положение по
времени. 2.
Сила – мера
воздействия одного тела на другое в
результате чего последнее приобретает
ускорение.3.
Траектория, Скорость, Ускорение.
Траектория
– она применяется в случае материальной
точки .Скорость
– отношение пути ко времени.
Ускорение
– первая производная от скорости 4.
Количество движения, Момент количества
движения и т.д.
Масса
и ее свойства:
Масса
- мера инертности тела; Инертность
– способность тела сохранять первоначальное
состояние. Состояние
– определяется
путем задания его положения и
скорость.
Свойства
массы.
1) Масса данного
тела является постоянной, не зависит
от времени, ни от скорости, ни от
местоположения. 2)
Аддитивность
масс – масса системы тел – сумма масс
тел входящих в систему 3)
Масса инертная
равняется массе гравитационной
31.Инерциальные
системы отчета и не инерциальные системы
отчета.
Законы
Ньютона
Система отчета.
Чтобы
задать закон движения нам нужна система
отчета и часы по которым определяем
момент времени и зависимость координат
по времени. Принцип
инерции Галилея.
Существуют
системы отсчета , относительно которых
свободное тело ( или действие сил на
которое скомпенсированно0 движется
равномерно и прямолинейно долго или
покоится. Всякая система отсчета, которая
движется относительно данной инерциальной
системы отсчета прямолинейно и равномерно
, тоже будет инерциальной системой
отсчета бесконечное множество.
РИСУНОК.
Переносное
ускорение – это ускорение точки
пространства системы k’,
где в данный момент находится материальная
точка обусловленное ускоренным
поступательным и вращательным движениями
k’.
РИСУНОК.
30.Введение
в динамику. Объекты и основные понятия
динамики. Сила. Масса.
Динамика
изучает движение объектов динамики с
учетом причин вызывающих изменения
движения, т.е. сил.
Объекты динамики:
1. Материальная
точка;2. Система материальных точек; 3.
Абсолютно твердое тело; 4. Система
абсолютно твердых тел
Материальная
точка – это
физическое тело размерами которого
можно пренебречь, по сравнению с размерами
области движения. Система
материальных точек
– совокупность материальных точек,
которые каким либо образом обособленны
от других материальных точек и других
тел. Абсолютно
твердое тело-
физическое тело, размеры и формы которого
остаются неизменными, тела не деформируемые.
Система
абсолютно твёрдых
тел- совокупность абсолютно твёрдых
тел, каким либо образом обособленных
от других тел.
Основные
понятия динамики являются:
1. Законы
движения –
зависимость координатных объектов,
которые определяют его положение по
времени. 2.
Сила – мера
воздействия одного тела на другое в
результате чего последнее приобретает
ускорение.3.
Траектория, Скорость, Ускорение.
Траектория
– она применяется в случае материальной
точки .Скорость
– отношение пути ко времени.
Ускорение
– первая производная от скорости 4.
Количество движения, Момент количества
движения и т.д.
Масса
и ее свойства:
Масса
- мера инертности тела; Инертность
– способность тела сохранять первоначальное
состояние. Состояние
– определяется
путем задания его положения и
скорость.
Свойства
массы.
1) Масса данного
тела является постоянной, не зависит
от времени, ни от скорости, ни от
местоположения. 2)
Аддитивность
масс – масса системы тел – сумма масс
тел входящих в систему 3)
Масса инертная
равняется массе гравитационной
31.Инерциальные
системы отчета и не инерциальные системы
отчета.
Законы
Ньютона
Система отчета.
Чтобы
задать закон движения нам нужна система
отчета и часы по которым определяем
момент времени и зависимость координат
по времени. Принцип
инерции Галилея.
Существуют
системы отсчета , относительно которых
свободное тело ( или действие сил на
которое скомпенсированно0 движется
равномерно и прямолинейно долго или
покоится. Всякая система отсчета, которая
движется относительно данной инерциальной
системы отсчета прямолинейно и равномерно
, тоже будет инерциальной системой
отсчета бесконечное множество.
РИСУНОК.

 Законы
Ньютона:
1
Закон:
Инерциальные системы отсчета существуют.
2 Закон:
Выполняется в ИСО и формулируется
так:
Ускорение тела прямо пропорционально
действующей на него силе и обратно
пропорционально массе.
3 Закон: Силы
взаимодействия двух тел равны по модулю,
противоположны по направлению
и имеют одну линию действия.
РИСУНОК.
Законы
Ньютона:
1
Закон:
Инерциальные системы отсчета существуют.
2 Закон:
Выполняется в ИСО и формулируется
так:
Ускорение тела прямо пропорционально
действующей на него силе и обратно
пропорционально массе.
3 Закон: Силы
взаимодействия двух тел равны по модулю,
противоположны по направлению
и имеют одну линию действия.
РИСУНОК.
 =
-
=
-
 32.Диферциональные
уравнения движения материальной точки
и системы материальных точек.
m
=
->
уравнения движения
=
(t)
x=
(t)
y=
(t)
z=
(t)
=
32.Диферциональные
уравнения движения материальной точки
и системы материальных точек.
m
=
->
уравнения движения
=
(t)
x=
(t)
y=
(t)
z=
(t)
= m
=
m
m
=
m =
= m
m =
=
 m
m =
=
 =
= +
+

 =
=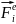 +
i=1,2,3,…,n
+
i=1,2,3,…,n
 =
= +
+
 33.Две
задачи динамики.
33.Две
задачи динамики.
1. Обратная задача
динамики, известно
-закон
движения
=
(H)
из её проекции
x=
(t)
y=
(t)
z=
(t)
Найти:
F-?
-?
-?
-?
Решение:
m
=
m
=
m
=
m
=
Использование производных.
Прямая
задача динамики: известно сила
=
(t,
,
)
Найти:
=f(t)
x=
(t)
y=
(t)
z=
(t)
Решение:
m
=
m
=
m
=
x=
(t, )
y=
(t,
)
y=
(t,
 )
z=
(t,
)
z=
(t, )
Начальное
условие: при t=0
x(0)=
)
Начальное
условие: при t=0
x(0)=

 (0)=
(0)= y(0)=
y(0)=
 (0)=
(0)= z(0)=
z(0)=
 (0)=
(0)= =
(
0,
=
(
0, )
=
(
0,
)
=
(
0,
)
=
(
0,
)
=
(
0, )
=
(
0,
)
=
(
0,
)
=
(
0,
)
=
(
0, )
=
(
0,
)
РИСУНОК.
Прямая задача динамики позволяет нам
по известному начальному состоянию с
помощью диф. уравнений движения найти
состояние материальной точки в любой
момент времени, в последующий или
предыдущий.
34.Частные
случаи интегрирования уравнения
движения
1Проекция зависит только
от времени
)
=
(
0,
)
РИСУНОК.
Прямая задача динамики позволяет нам
по известному начальному состоянию с
помощью диф. уравнений движения найти
состояние материальной точки в любой
момент времени, в последующий или
предыдущий.
34.Частные
случаи интегрирования уравнения
движения
1Проекция зависит только
от времени




