- •Предмет статика. Основные понятия статики.
- •Сила. Система сил. Силы сосредоточенные и распределенные.
- •Аксиомы статики и их следствия.
- •16.Трение скольжения. Равновесие при наличии трения скольжения.
- •17.Трение качения. Равновесие при наличии трения качения.
- •2Проекция зависит только от скорости Для остальных координат все тоже самое только вместо х у или z
- •2 Закон Ньютона.
- •47. Постановка задачи о движении несвободной материальной точки, системы материальных точек. Связи. Классификация связей.
- •50. Принцип возможных перемещений.
- •51. Обобщенные координаты. Обобщенные силы.
- •52. Принцип Даламбера и Даламбера-Лагранжа.
Предмет статика. Основные понятия статики.
Статикой называется раздел механики, в котором излагается общее учение о силах и изучаются условия равновесия материальных тел, находящихся под действием сил. Объектом статики являются абсолютно твердое тело и система абсолютно твёрдых тел. Абсолютно твердое тело- физическое тело, размеры и формы которого остаются неизменными, тела не деформируемые. Система абсолютно твёрдых тел- совокупность абсолютно твёрдых тел, каким либо образом обособленных от других тел.
Криволинейный шатунный механизм. РИСУНОК Движение мохового колеса приводит в движение поршень, и наоборот, и они могут находиться в равновесии, быть неподвижными.
Статика изучает условие равновесия абсолютно твёрдых тел и систем абсолютно твёрдых тел.
Сила. Система сил. Силы сосредоточенные и распределенные.
Сила в статике
определяется следующим образом:
Сила это мера
воздействия одного тела на другое в
результате чего одно тело испытывает
деформацию.
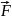 -сила,
-сила,
 сила реакции поверхности,
сила реакции поверхности, сила
натяженя нити(троса),
сила
натяженя нити(троса),
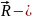 Равнодействующая
сила,
Равнодействующая
сила,
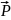 ,
,
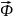 -
сила инерции. Линия
вдоль которой
действует сила- называется линией
действия силы.
-
сила инерции. Линия
вдоль которой
действует сила- называется линией
действия силы.
Система сил- это
совокупность нескольких сил, приложенных
к абсолютно
твёрдому телу и к системе абсолютно
твёрдых тел. Обозначается
{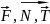 }
Системы сил можно квалифицировать:
}
Системы сил можно квалифицировать:
Сходящаяся система сил- это система сил, линии действия которых пересекаются в одной точке.
РИСУНОК 2)Система параллельных сил- это система сил линии действия которых параллельны РИСУНОК
3)Плоская
система сил-
система сил линии действия которых
лежат в одной плоскости. Плоскую систему
сил можно детально анализировать: а)
Плоская сходящаяся
система сил-линии действия в одной
плоскости и пересекаются в одной точке.
б)Плоская
параллельная
система сил-пересекается в одной
плоскости и параллельны в)Плоская
произвольная
система сил-линии действия лежат в одной
плоскости, но не пересекаются в одной
точке и не параллельны.
4)Пространственная
система сил-
система сил линии действия которой
лежат в пространстве:
а)
Пространственная сходящаяся система
сил – линии действия лежат в пространстве,
но в одной точке пересекаются
б)
Пространственная параллельная система
сил- линии действия лежат в пространстве,
но между собой параллельны
в)
Пространственная произвольная система
сил- линии действия которой лежат в
пространстве, но никаких закономерностей
нет, не сходятся в точке и не параллельны.
Силы делятся
на сосредоточенные и
распределенные:
Сосредоточенная
сила- это
сила приложена в точке и действует в
определенной точке. Распределенная
сила- это
сила называется нагрузками: могут быть
распределены: 1)вдоль
линий кривых-линейные
2)вдоль
поверхностей(
не плоских)-поверхностные 3)по
объёму-
объемные
В общем случае определить
нагрузки не просто. Частные
случаи: Если
линейная нагрузка-
линейная однородная, сила распределяется
вдоль прямой и равномерно РИСУНОК
q-линейная
однородная нагрузка
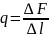 [q]-
[q]-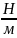
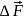 =
=
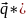
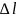 q=
lim(
q=
lim(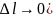
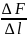 =
=
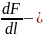 неоднородная
нагрузка
неоднородная
нагрузка
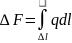 Однородная
поверхностная нагрузка-
нагрузка распределена равномерно
Однородная
поверхностная нагрузка-
нагрузка распределена равномерно
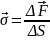
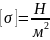
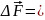
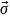 *
*
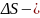 Однородная нагрузка; Объёмная
нагрузка f:
Однородная нагрузка; Объёмная
нагрузка f:
 =
=
 [ f
]-
[ f
]-
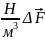 =
*
=
*