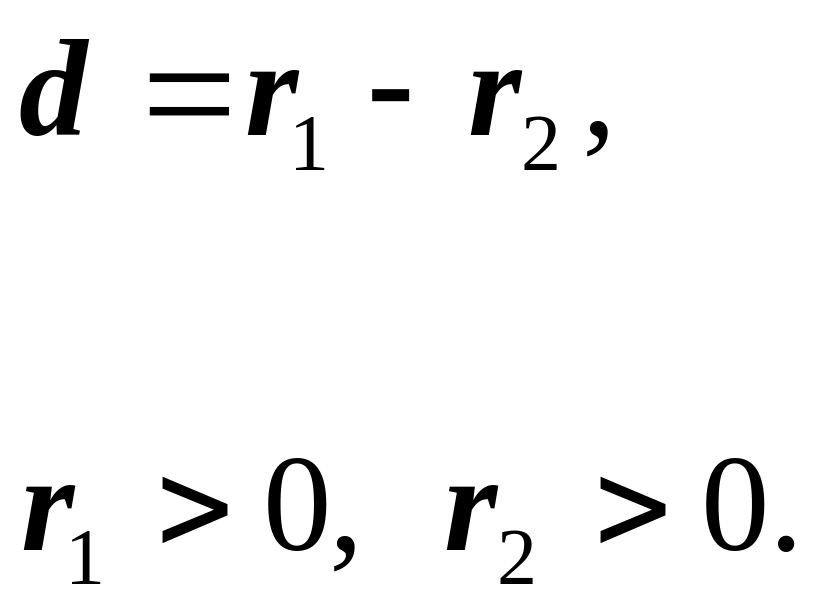8. Различные виды линз.

Все линзы делятся на две группы.

Первую группу составляют линзы, имеющие положительные задние фокусные расстояния. Такие линзы называются положительными. Вторую группу составляют линзы, имеющие отрицательные фокусные расстояния. Эти линзы называются отрицательными. Положительные линзы являются собирательными, а отрицательные рассеивающими.

Рассмотрим более подробно группу положительных линз.

1. Двояковыпуклая линза (рис 1.20,а).

Ее конструктивные элементы: 

Из формул (1.43) и (1.40) получим

Главные плоскости у таких линз лежат внутри линзы.

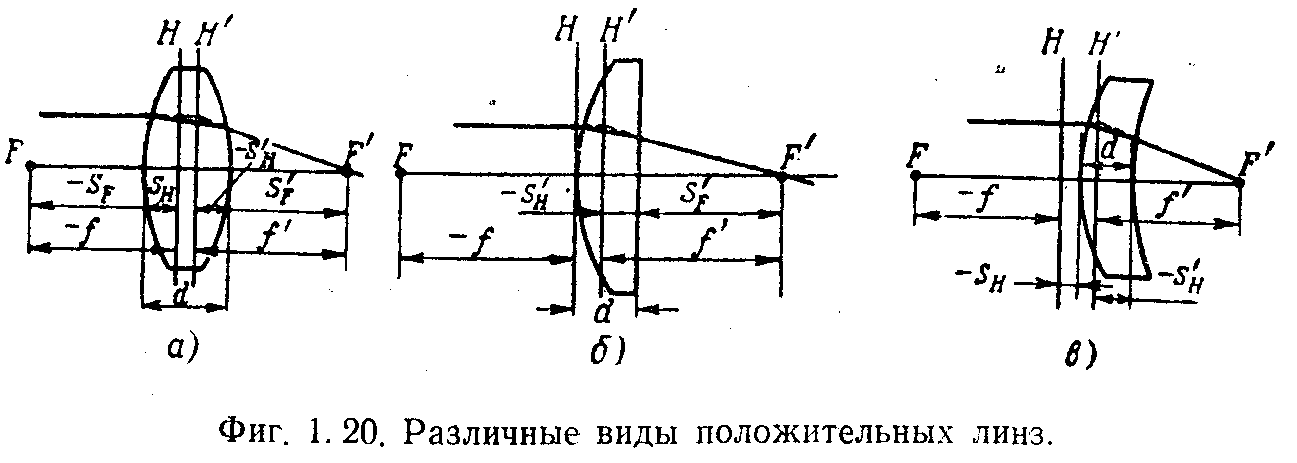
В частном случае, когда , линза называется симметричной.

2. Выпукло-плоская линза (рис 1.20,б).

Из формул (1.38) - (1.43) получим

Следовательно, фокусное расстояние такой линзы не зависит от толщины линзы, а главные плоскости лежат внутри линзы и одна из них касается выпуклой поверхности.

3. Выпукло-вогнутая линза (рис 1.20,в)

(называется менисковой)

 

Из формул (1.43) и (1.40) следует

Значит, передняя главная плоскость лежит вне линзы. Можно подобрать такие значения r₁ и r₂, когда обе главные плоскости будут расположены вне линзы.

Соответствующие три вида имеют и отрицательные линзы (рис 1.21).

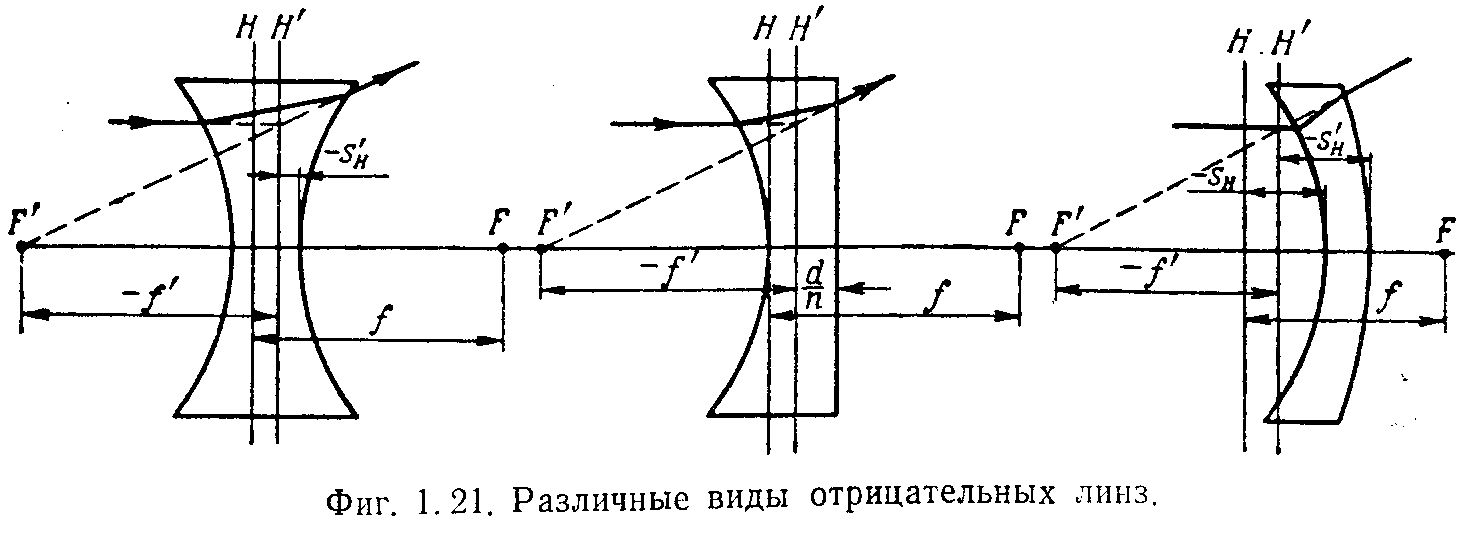
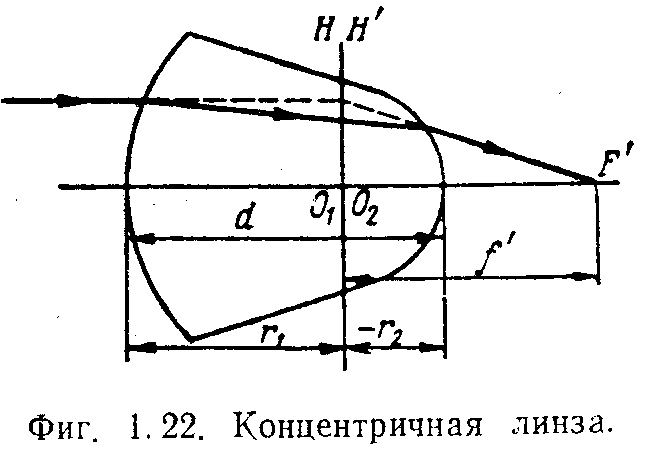
4.Концентричная линза.

Концентричной называется такая линза, у которой центры кривизны О1 и О2 обеих поверхностей совпадают (рис 1.22)

В этом случае толщина линзы равна

Из формул (1.38), (1.40), (1.43) находим

т.е. главные плоскости в таких линзах совпадают и проходят через общий центр кривизны обеих поверхностей.

5. Шаровая линза

 Из формулы (1.38) получим

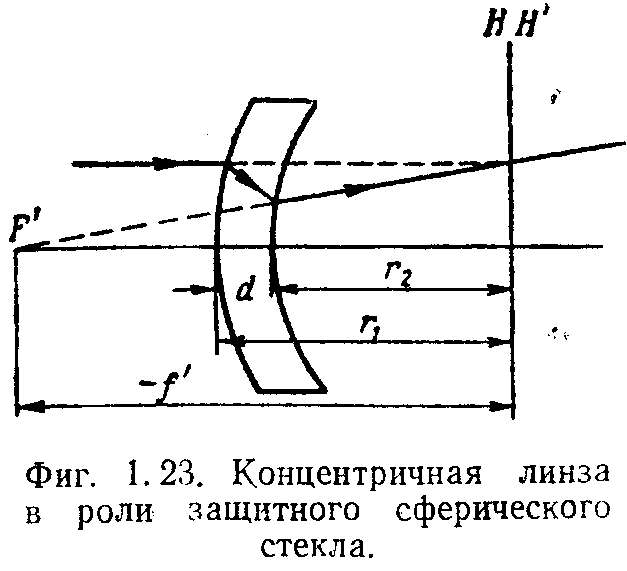
6. Сферическое защитное стекло приборов.

 В качестве защитных стекол приборов иногда применяется концентричная линза (рис 1.23)

Из формулы (1.38) найдем

т.е. такое стекло является отрицательной линзой.

9. Определение радиусов кривизны преломляющих

поверхностей при заданном ходе параксиального луча.

Пусть ход параксиального луча через систему преломляющих поверхностей задан (см.рис.1.10). Следовательно, заданы следующие параметры:

При этом соблюдается зависимость

Согласно формуле (1.15) получим:

По формуле (1.45) можно найти значение радиусов кривизны поверхности, обеспечивающих заданный ход луча.

В качестве примера решим задачу (см.рис.1.24).

Пусть известны следующие параметры:

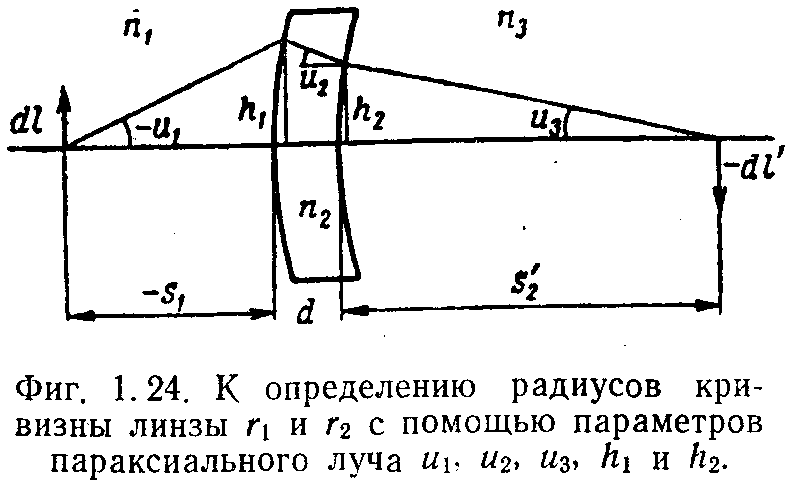
Из данных условий находим

Пусть u3 = 0.1, тогда

Радиусы кривизны вычислим по формуле (1.45), перепишем ее условно так:

Для удобства вычислений воспользуемся табл.1.2

k	uk
1	-0.2	1	-0.2	0.32	0.5	1.56	12	18.7
2	0.08	1.5	0.12	-0.02	-0.5	25	11.5	287
	0.1	1	0.1

Получим следующие результаты: