6. Определение положения и величины изображения, образуемого оптической системой, у которой известны положения фокусов и главных точек
Пусть дана оптическая система, состоящая из ряда преломляющих поверхностей, положения фокусов и главных плоскостей которой известны, а стало быть, известны и фокусные расстояния (рис 1.18).
Возьмем предмет dl, находящийся от переднего фокуса F системы 1-р на расстоянии х, а от передней главной точки Н на расстоянии а. Отрезки х и а имеют начало отсчета в точках F и Н.
Найдем положение изображения dl'.
Решим сначала эту задачу графическим способом. Построим изображение точки С - вершины заданного отрезка dl. Для этого достаточно взять любые два луча, выходящие из точки С, и найти точку их пересечения по
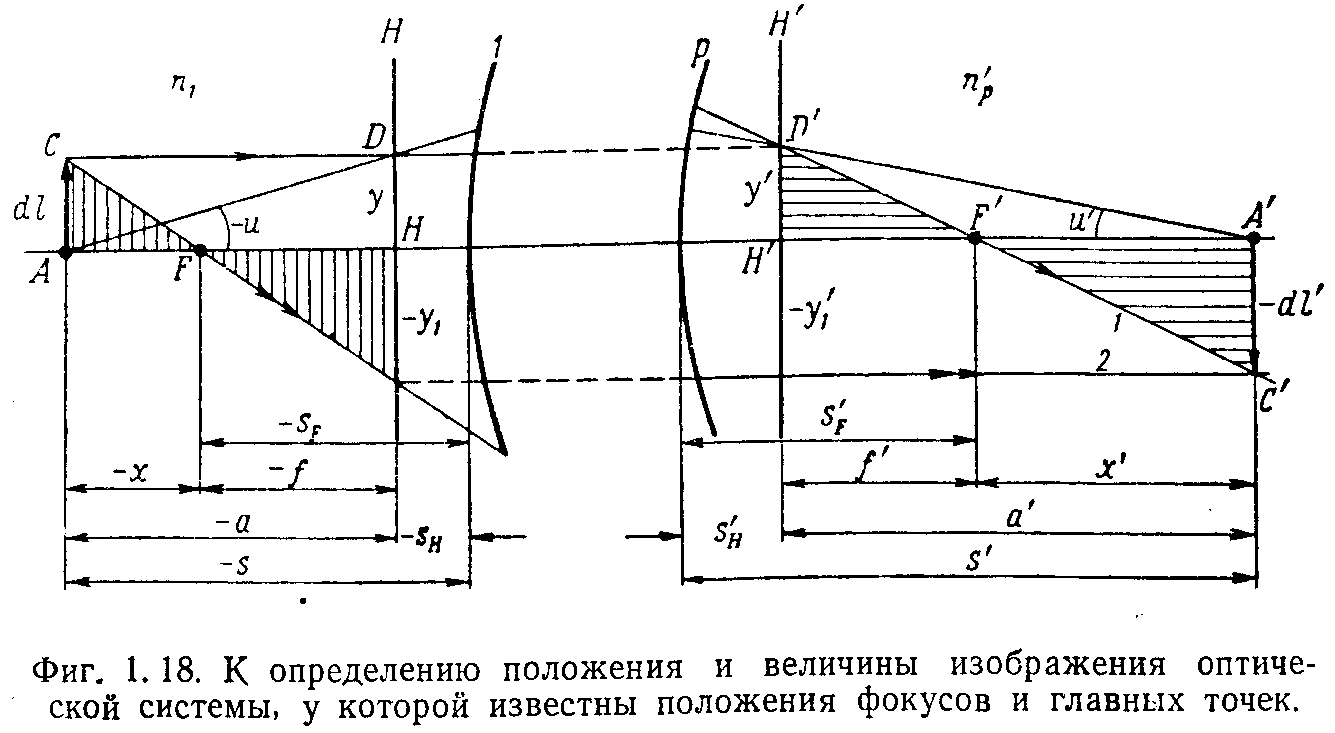
выходе из системы. Пусть луч СD идет параллельно оси, этот луч по выходе из системы пройдет через задний фокус F', причем у' = у = dl. Второй луч CF идет через первый фокус F и, следовательно, по выходе из системы будет параллелен оптической оси, при этом -y = -y' = -dl'. Точка С' пересечения этих лучей определяет положение и величину изображения отрезка dl'.
Из подобия треугольников получим
(1.34)
откуда
(1.35)
или, заменяя х = a - f и x' = a'- f', найдем
(1.36)
Формулы (1.35) и (1.36) дают возможность определить положение изображения, зная положение предмета. Формула (1.35) носит название формулы Ньютона, а формула (1.36) - Гаусса.
Проведем теперь луч из точки А под некоторым углом к оси через точку D. Из фигуры следует, что
u = Y/a , u'= Y'/a'= Y/a'
Если теперь воспользоваться формулами (1.14) и (1.34), то получим следующую формулу для линейного увеличения:
(1.37)
Таким образом, по формуле (1.37) можно вычислить величину изображения:
dl'
= dl
Положение же изображения относительно последней преломляющей поверхности S' определяется с помощью формул (1.35) и (1.36), а именно:
S'= S'F + x'
или
S' = S'H + a'
Таким образом, если имеется сложная оптическая система с заданными конструктивными элементами и требуется найти положение и величину изображений ряда по разному расположенных предметов, то выгоднее сначала найти положение фокусов и главных плоскостей, а затем уже решать поставленные задачи по методике, изложенной в данном параграфе.
7. Одиночная линза в воздухе.
Рассмотрим
одиночную линзу, находящуюся в воздухе,
и определим зависимость фокусного
расстояния от её конструктивных элементов
(фиг. 1.19).
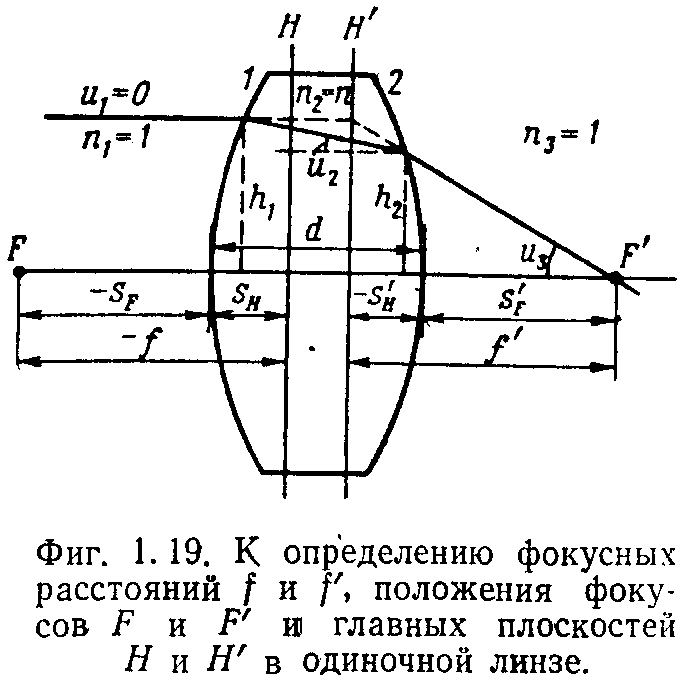
Для этого, применяя формулы (1.15) и (1.16), произведем расчет хода луча через линзу, полагая u1 =0, n1 = n3 =1; величина h выбрана произвольно.
Из указанных формул следует:
;
;
.
и, следовательно, согласно формуле (1.25)
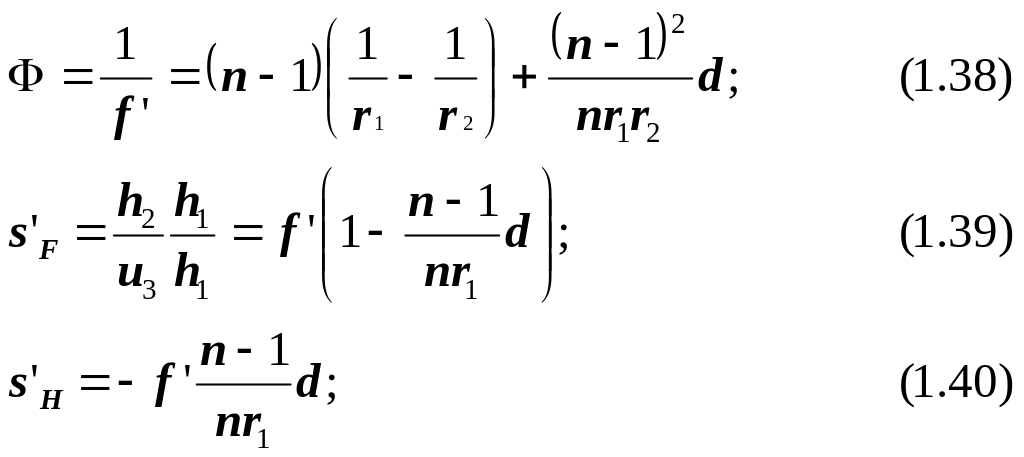
Рассчитав ход такого же луча справа налево, получим:
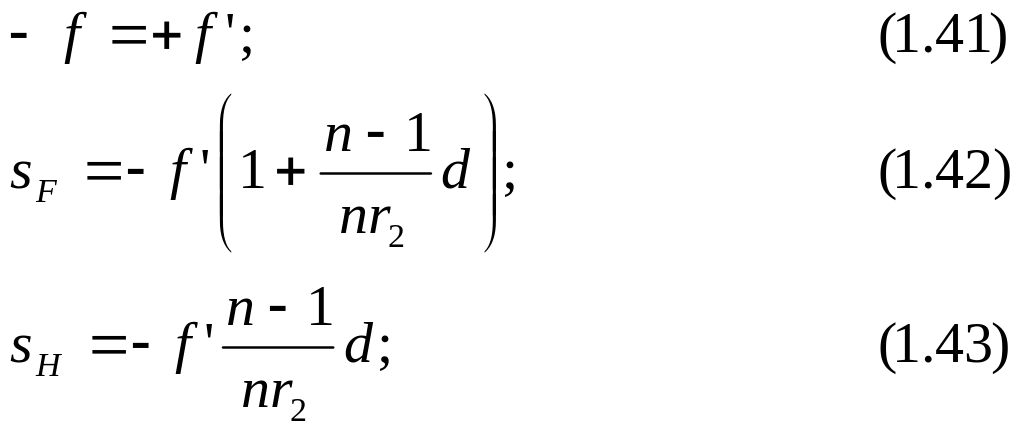
Если расстояние между вершинами поверхности d значительно меньше величины радиусов кривизны, то вторым слагаемым в формуле (1.38) можно пренебречь, и эта формула для тонкой линзы примет более простой вид:
Например пусть линза имеет следующие конструктивные элементы:
Фокусное
расстояние линзы, вычисленное по формуле
(1.38),будет равно
.
Если
линзу считать тонкой и ее фокусное
расстояние вычислить по формуле (1.44),
то получим
.
Ошибка составит
,
т.е. 2%. Поэтому в практических расчетах
чаще пользуются приближенной формулой
(1.44) и лишь при точных вычислениях
применяют формулу (1.38).
Пользуясь формулами (1.40) и (1.43), можно определить расстояние НН' между главными плоскостями в линзах. Согласно рис 1.19 имеем
откуда
или, подставляя вместо sH и s'H их значения из формул (1.40) и (1.43),получим:
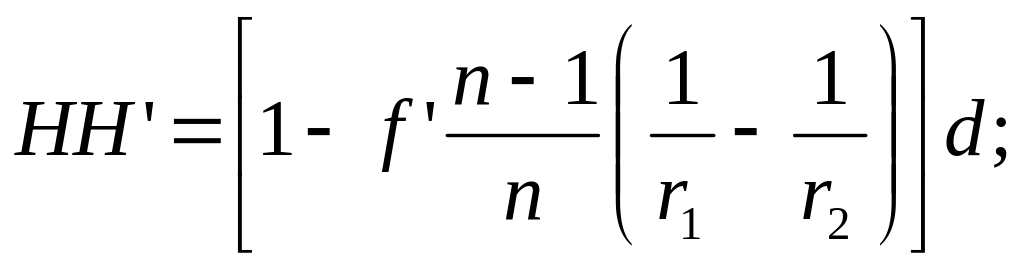
для бесконечно тонкой линзы
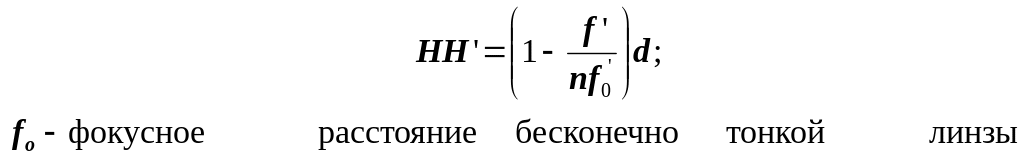
Если толщина линзы не слишком велика и линза не является менискообразной, то вполне можно положить
f'0 = f'
тогда получим формулу, наиболее приемлемую для практических расчетов:
Т.к. показатели преломления n стекол лежат в пределах от 1.45 до 1.9, то для различных n получим следующий ряд значений НН' при d=1 мм.
n . . . 1,45 1,5 1,55 1,6 1,7 1,8 1,9
HH'. . . 0,31 0,33 0,35 0,37 0,41 0,44 0,47
Часто положительные линзы делаются с показателем преломления n=1,52. Для таких линз
HH'
(1/3)d.