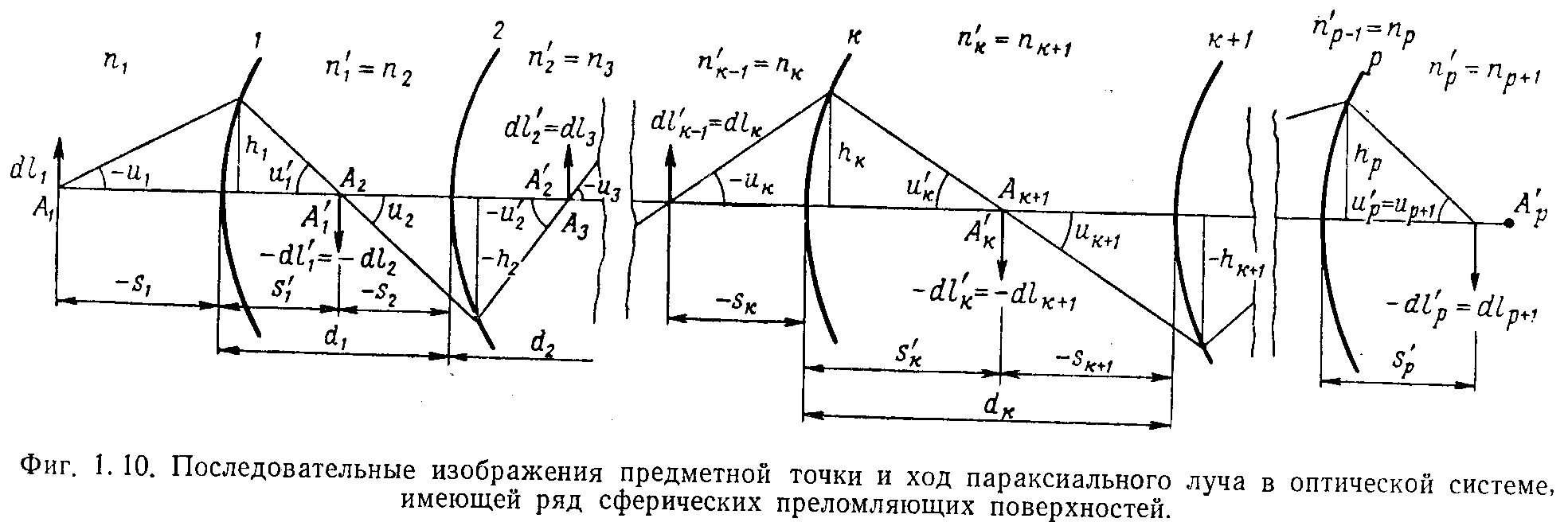
Изображение в оптической системе,состоящей из ряда
СФЕРИЧЕСКИХ ПОВЕРХНОСТЕЙ.
Рассмотрим образование изображений в параксильной области оптической системы, состоящей из ряда сферических поверхностей 1, 2, ... к, ...р. (рис 1.10).
Т.к. изображение любой предметной точки является в свою очередь предметом для последующей поверхности, то исходя из фигуры можно записать:
,
…
.
,
…
.
Кроме того:
,
…
,
…
и т. д. Из формулы (1.12), применяя ее к каждой из преломляющих поверхностей, получим
(1.13)
Формула (1.13) дает возможность определить линейное увеличение для всей системы:
(1.14)
Для
определения положения и величины
изображения
рассмотрим два способа:
1 способ основан на расчете хода луча, вышедшего из предметной точки через оптическую систему. Для вывода расчетных формул воспользуемся рис 1.10 и формулой (1.9).Умножим обе части формулы (1.9) на величину h ,обозначающую высоту пересечения луча с поверхностью:
Производя замену:
;
окончательно получим
(1.15)
Из рис 1.10 также следует (для параксиальной области)
(1.16)
Зная для выбранного луча входные координаты u и h, причем
и применяя последовательно к каждой из поверхностей формулы (1.15) и (1.16), найдем все значения углов и высот:
u = u = u = … u'=
1 2 3 p
h = h = h = … h =
1 2 3 p
Таким образом, положение изображения s', линейное увеличение и величина изображения dl' определяется по формулам
(1.17)
(1.18)
(1.19)
2 способ - последовательное применение формулы (1.9)к каждой из поверхностей (на рис 1.10).
Применительно к поверхности k эта формула примет вид:
(1.20)
и
.
В результате этих расчетов мы найдем значения всех отрезков, определяющих положения промежуточных изображений, т.е. будут известны отрезки
.
Линейное увеличение в этом случае лучше рассматривать как произведение линейных увеличений отдельных поверхностей; принимая во внимание формулу (1.11), получим:
(1.21)
Таким образом будут найдены положение и величина изображения, т.е.
и
Формулы (1.15) - (1.21) позволяют определить основные свойства оптической систем (положение и величину изображения).
В качестве иллюстрации приведем пример расчета хода луча через простую линзу:
r1 = 18.7 d1 = 6 n1 = 1
r2 = 287 n2 = 1.5 n3 = 1
Расстояние от линзы до предмета s = -60. Выберем произвольно u = - 0.2. Тогда для высоты входного луча из первой поверхности получим
Применяя формулы (1.17) и (1.18), вычисления удобно производить с помощью калькулятора или микроЭВМ.
Положение изображения и линейное увеличение определяться по формулам:
