23. Сравнение рассмотренных сортировок

Качественная оценка:

- сортировка пузырьком

- шейкер-сортировка

- сортировка выбором

- сортировка вставками

- сортировка вставками с барьером

- сортировка Шелла

23. Пирамидальная сортировка

Пирамида (heap) – бинарное дерево высота k, в кот. :

1. Все узлы имеют глубину k или k-1

2. При этом уровень k-1 полностью заполнен, а уровень k заполнен слева направо

3. Выполняется «свойство пирамиды» каждый эл-т меньше, либо равен родителю

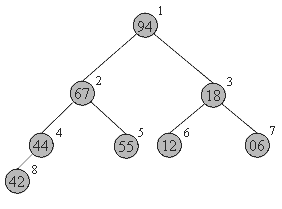
Соответствие между геометр.структурой пирамиды как бинарн.дерева и массивов устанавливается по схеме:

1. В а[0] хранится корень дерева

2. Левый и правый сыновья а[i] хранятся соответственно в а[2i+1] и a[2i+2]

Таким образом для массива, хранящего в себе пирамиду, выполняется характеристическое свойство:

a[i] >= a[2i+1] и a[i] >= a[2i+2].

23. Быстрая сортировка.

1970г. Является одной из более широко применяемых и эффективных сортировок.

Схема алгоритма:

1. Из массива выбирается опорный эл-т a[i]

2. Запускается процедура разделения массива, кот перемещает все эл-ты меньшие либо равные a[i] в левую часть, а элементы >= в правую часть

3. Теперь массив состоит из двух подмножеств

4. Для обоих подмассивов, если в подмассиве больше двух эл-тов, рекурсивно выполняется та же процедура разделения массива

Разделение массива:

На входе массив a[0] … a[n], опорный эл-т p.

1. Введем два индекса i и j. В начале они указывают соответственно на левый и правый эл-т последовательности

2. Будем двигать указатель I, i++ в право до тех пор, пока a[i]>=p, затем аналогичным способом двигаем j, j--. Ищем a[j]<=p

3. Если i<=j, меняем a[i] и а[j] местами и продолжаем двигать a[i] и a[j] по тем же правилам

Повторяется шаг 3, пока i<=j

23. Сортировка слиянием

Принцип примерно такой же как и быстрой сортировке, вместо разделения по опорному эл-ту, массив просто делится пополам

a - сортируемый массив, его левая граница lb, правая граница ub

void mergeSort(int a[], long lb, long ub) {

long split;

if (lb < ub) {

split = (lb + ub)/2;

mergeSort(a, lb, ub);

mergeSort(a, split+1, last);

merge(a, lb, split, ub); } }

23. Графы – основные понятия.

ГрафG(V,E) - совокупность двух множеств – непустого множества V (множества вершин) и множества E(множества ребер) неупорядоченных пар различных элементов множества V

G(V,E) = {V,E}, V , EVV, E=E^-1.

Число вершин графа G- p, а число ребер– q:

p = p(G) = |V|, q = q(G) = |E|.

Пусть v1, v2 – вершины, e=(v1,v2) – соединяющее их ребро. Тогда вершина v1 и ребро e инцидентны, вершина v2 и ребро e также инцидентны. Два ребра, инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также назыв. смежными

Множество вершин, смежных с вершиной v, называется множеством смежности вершины v и обозначается

Г (v): Г (v) = {uV | (u,v)E}

Если элементами множества E являются упорядоченные пары, то граф называется ориентированным (или орграфом). В этом случае элементы множества V называются узлами, а элементы множества E – дугами

Если элементом множества E может быть пара одинаковых элементов V, то такой элемент E называется петлей, а граф называется графом с петлями (или псевдографом).

Если E является не множеством, а набором, содержащим несколько одинаковых элементов, то эти элементы называются кратными ребрами, а граф называется мультиграфом.

Если задана функция F:VM и/или F:EM, то множество M называется множеством пометок, а граф называется помеченным.

Маршрутом в графе называется чередующаяся последовательность вершин и ребер v₀,e₁,v₁,e₂,v₂,…,e_k,v_k, в которой любые два соседних элемента инцидентны.

Для обычных графов достаточно просто перечислить либо последовательность вершин либо ребер. Если v₀=v_k, то маршрут замкнут, в противном случае – открыт.Если все входящие в маршрут ребра различны, то маршрут называется цепью.

Длиной маршрута называется количество ребер в нем (с повторениями). Расстоянием между вершинами u и v (обозначается d(u,v)) называется длина кратчайшей цепи {u,v}

Две вершины в графе связаны, если существует соединяющая их цепь. Граф, в котором все вершины связаны, называется связным.