16. Кольцевые списки.

Кольцевой список — это список, у которого последний элемент связан с первым. Кольцевой список можно сделать как односвязным, так и двухсвязным. Рассмотрим вкратце односвязный кольцевой список.

Кольцевой список не имеет первого и последнего элемента. Кольцевые списки также подразделяются на однонаправленные списки  и двунаправленные. В программе, работающей со списком, обычно заводят четыре служебных переменных,  lenth        – число узлов в списке; listbeg – указатель на первый узел в списке;  listend – указатель на последний узел в списке; current – указатель на обрабатываемый узел.

Число служебных переменных иногда может быть и больше, и меньше: все зависит от назначения создаваемой программы.

17. Многосвязные (слоеные) списки.

В одном элементе списка может быть задано сколько угодно связей для того, чтобы при выборке заданного подмножества информационного поля не выполнять полный просмотр, в каждую запись включается дополнительное поле ссылок, каждая из которых связывает в линейный список элементы соответствующего подмножества. В результате каждая подзадача работает со своим подмножеством как с линейным списком.

Специфика слоеного списка проявляется только в операции исключения (исключение эл-та из какого-либо списка не означает необходимость удаления эл-та из памяти, т.к он может оставаться в составе других списков)

18. Поиск.

Массив А элементов – множество данных, в котором имеется элемент, является фиксированным.

Искомый элемент – образец Х.

Если нет дополнительной информации о разыскиваемых данных, то самый простой способ – это последовательный просмотр элементов массива (линейный поиск). Условия окончания линейного поиска:

1. Элемент найден (a[i]=x)

2. Массив просмотрен, ничего не обнаружено

Алгоритм 1: i=0;

while((i<N)&&(a[i]!=x))i++;

Алгоритм 2: a[N]=x; i=0;

while(a[i++]!=x); //поиск с барьером

Если i=N, то эл-та в массиве не существует.

19. Бинарный поиск.

Бинарный поиск состоит в том, что ключ V сравнивается со средним элементом списка. Если эти значения окажутся равными, то искомый элемент найден, в противном случае поиск продолжается в одной из половин списка.

Если больше нет никакой доп.информации, то поиск нельзя улучшить, но если известно что-либо, то поиск можно ускорить.

Если данные упорядочены, то скорость поиска можно повысить.

Идея: выбрать случайный эл-т. Сравнить его с искомым Х.

Если он совпадает, то поиск заканчивается

Если <X, то все эл-ты с индексом <=m из дальнейшего рассмотрения можно исключить.

Если X>a_m, то из рассмотрения можно исключить индексы >=m.

Это поиск деления пополам.

В результате max число сравнений ln(N) округлится до ближайшего целого.

int Find (int* A, int N, int X){

int m, L=0, R=N-1, flag=0;

while (L<=R && !flag)

{ m=(L+R)/2;

if (A[m]==X) flag = 1;

else if (A[m]<X) L=m+1;

else R=m-1;

}

return flag; }

20. Алгоритм прямого поиска.

Пусть задали массив S[ ] из N элементов и массив P[ ] из M эл-тов. Поиск строки обнаруживает 1-ое вхождение P в S (0<M<=N). S – некоторый текст, а P – слово.

Результатом поиска является индекс i, указывающий на первые от начала строки совпадения с образцом.

i=-1;

do

{ i++; j=0;

while ((j<M) && (s[i+j] == p[j]) ) j++;

&& P(i,j) && ((j==M) || s[i+j]!= p[j]))

} while (j<M && i < N-M);

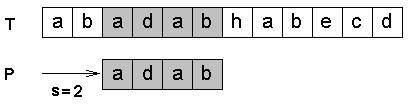
число операций = N*m, где m – число слов в тексте, N – число букв в слове.