Линейные списки – основные операции.
Линейный список – список, отражающий отношение соседства между элементами.
Операции:
Создание списка
Заключается в определении указателя начала списка и присвоении ему значения NULL
Перебор элементов списка.
Эта операция выполняется для линейных списков очень часто и состоит в последовательном доступе к элементам списка – ко всем до конца списка либо до нахождения искомого элемента. Для каждого из перебираемых элементов осуществляется некоторая обработка его информационной части: сравнение с образцом, печать, модификация и прочее.
Вставка элемента в список.
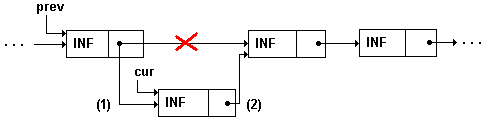
Вставка элемента в середину односвязного списка
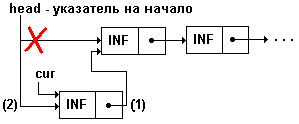
Вставка элемента в начало односвязного списка
Удаление эл-та из списка
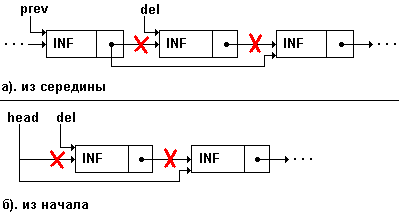
Перестановка соседних элементов односвязного списка
Реализ списков на основе динам стру.
#include<stdio.h>, <stdlib.h>
#include<locale.h>, <conio.h>
struct date { int day; };
struct node { date data;
node *next; };
void getData(node *p) {
do { printf("День даты\n");
} while (!scanf("%d", &p->data.day)||p->data.day < 1||p->data.day > 31);
void insert(node **start) {
node *p = new node;
getData(p);
if(!*start){ p->next = NULL;
*start = p;
return;}
node *prev=*start,*post=*start;
while (post){
if(post->data.day>p->data.day)
{ p->next = post;
if (post==*start)*start= p;
else prev->next = p;
return; }
prev = post;
post = post->next;}
p->next = NULL;
prev->next = p;}
node *find(node*start,int dat){ node *p = start;
while (p){
if (p->data.day == dat)
return p;
p = p->next; }
return false;}
node*remov(node**start,int dat) { if(!*start) return false;
node *pdat;
pdat = find(*start, dat);
if (pdat){
if (pdat == *start)
*start = (*start)->next;
Else {
node *prev = *start;
while (prev){
if (prev->next==pdat)break;
prev = prev->next;}
prev->next = pdat->next;}
return pdat;}
return false;}
void print(node *start) {
node *p = start;
while (p){
if (p==start) printf ("День");
printf ("%d\n", p->data.day);
p = p->next;} }
Двусвязный список и его программная реализация.
Двусвязный список позволяет выполнять «движение» от элемента к элементу в обоих направлениях. В этом случае элемент включает два указателя: на предыдущий и последующий элементы списка. А так как список имеет и начало, и конец, описываются еще два указателя – начала и конца списка
#include"stdafx.h","conio.h"
#include"iostream","locale.h"
struct node { int info;
node *next; }
void 1(node**begin,node**end)
{ node *temp = new node;
p->info=rand();
p->next=NULL;
*begin=*end=p; }
void AddQ(node **end){
node *p = new node;
p->info=rand()%100;
(*end)->next=p;
p->next=NULL;
*end=p;}
void DelQ(node *begin, node **end) {
node *p=begin;
if(*begin==*end)
*begin==*end=NULL;
else *begin=p->next;
delete p;}
void printQ(node *begin){
node *p=begin;
while(p){
printf("%d ", p->info);
p=p->next;} }
void DellAllQ(node **begin, node **end){
node *p;
while(begin->next!=NULL){
p=begin->next;
begin->next = begin->p;
delete p;}
*end=begin; }