2.4 Общие решения уравнения диффузии в средах

Прежде всего, ограничимся пока стационарным уравнением диффузии

Q(r)+∇ [D(r) ∇Ф(r)] –Ф(r)*Σ_а (r) =0

Где r- координата.

Далее, отметим, что в средах с размножением нейтронов источник Q(r) следует рассматривать как сложный оператор, состоящий собственно из интенсивности спонтанно испускаемых нейтронов и скорости реакции деления, интенсивность которой зависит от потока в среде, то есть

Далее, для простоты предположим что коэффициент диффузии не зависит от координат(его можно вынести за знаки операторов набла:

+D∇ [∇Ф(r)] –Ф(r)*Σ_а (r) +Ф(r)*ν_fΣ_f (r)=-Q (r) (2.10a)

+D ∇ [∇ Ф(r)] + Ф(r)*{ -Σ_а (r) +ν_fΣ_f (r)}=-Q (r) (2.10б)

Разделив его на Dи вынося за скобки Σ_а (r)получим :

Σ_а (r)

+ ∇ [∇ Ф(r)] + Ф(r)*{ ν_fΣ_f (r)/ Σ_а (r) -1}=-Q (r)/D (2.10в)

Величина

ν_fΣ_f (r)/ Σ_а (r)= К_∞ , (2.11а)

которая описывает отношениескорости генерации нейтронов к скорости их поглощения называется «коэффициентом размножения бесконечной среды» К_∞(или упрощенно «бесконечным коэффициентом размножения» среды ) для моноэнергетических нейтронов.

Вообще, более общим (и простым) является определение «эффективного коэффициента размножения» в терминах популяций и поколений:k_эф есть отношение числа нейтронов в данном поколении «i+1» к числу нейтронов в предыдущем поколении «i»:

k_эф = N_i+1 / N_i (2.11в)

Введем понятие «квадрат длины диффузии»:

L² = D/ Σ_а=1/(3 Σ_а.Σ_tr) (2.11с)

размерность L²- см²_.

Тогда 2.10в) можно записать как:

+ ∇ [∇ Ф(r)] + Ф(r)*{ К_∞-1}=-Q (r)/D (2.10г)

Наконец, для решения задачи уравнений математической физики введем свободный параметр Λ=1/К_эфф в форме К_∞/К_эфф, где К_эфф–«эффективный коэффициент размножения» ограниченной среды или реактора .

Тогда получим

+ ∇ [∇ Ф(r)] + Ф(r)*{ К_∞/К_эфф-1}=-Q (r)/D (2.10д)

Возможность решения его и получаемые функции будут зависеть от знака в фигурных скобках, наличия источника и граничных условий.

Введем понятие «материального параметра среды» æ_м² и определим его как:

æ_м² =1/L²{ К_∞/К_эфф-1}= 1/L²{ ν_fΣ_f / K_эффΣа-1} (2.11в)

размерность æ_м²- 1/см²_,

Формула для L²с учетом размножения может быть обобщена:

L² = D/ [Σ_а(1- К_∞)] (2.11г)

С точки зрения знака выражения в фигурных скобках условно разделим среды на:

«неразмножающие», точнее «слаборазмножающие» если:

1/L² { ν_fΣ_f / K_эффΣа -1} <0 или{ К_∞/К_эфф-1} <0 илиК_∞<К_эфф

В таких средах размножение нейтронов за счет деления недостаточно для поддержания профессионально т.н. «самоподдерживающейся цепной реакции СЦР».

1/L² { ν_fΣ_f / K_эффΣа -1} >=0 или { К_∞/К_эфф-1} >=0 илиК_∞>= К_эфф

В таких средах размножение нейтронов за счет деления уже достаточно для поддержания «самоподдерживающейся цепной реакции СЦР».

Соответственно для этих случаев получение решений и условия их существования будут различны.

Вариант 1 «Слаборазмножающая среда».æ_м²<0.

Уравнение имеет вид для Σ_f =0

∇ [∇ Ф(r)] - Ф(r) =-Q (r)/D (2.12а)

Необходимым условиям существования стационарного решения для такой среды является наличие ненулевогоисточника Q( r).

Класс получаемых решений будет:

Ф(r)=C₁exp(+r/L) + C₂exp(-r/L) (2.12.в)

Или подобные им функции Бесселя(для цилиндрической геометрии). Коэффициенты С (или функции C*(1/r) определяются из условий нулевых значений функций на бесконечности и мощности источника. Как правило, часть решения с неограниченно возрастающей экспонентой мы отбрасываем и С₁ приравниваем нулю.

Проиллюстрируем решение на примере одномерной геометрии (бесконечной плоскости).Если вообразить бесконечный плоский источник тепловых нейтронов равномерной интенсивности (чего в природе нет!), то, приложив вплотную к этому источнику некоторый объём рассматриваемой среды (вещества), мы обнаружили бы, что плотность потока тепловых нейтронов с удалением от источника в этой среде падает по экспоненциальному закону (рис.2.3):

Ф(x) = Ф_оexp (- x/L)

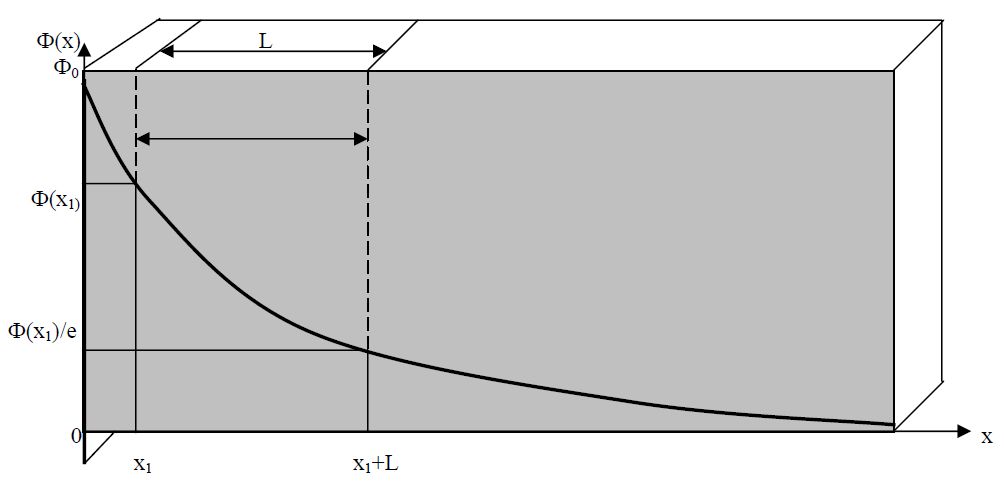
Рис. 2.3. Плотность потока тепловых нейтронов с удалением от источника

Поэтому, если измерить величину плотности потока тепловых нейтронов на произвольном расстоянии X₁от источника и на расстоянии (x₁+L), то отношение измеренных величин плотностей потоков тепловых нейтронов будет равно:

Ф(х₁)/Ф(х₁+L) = exp(-х₁/L)/exp[-(x₁+L)/L] = е = 2.7182818...

Отсюда следует физический смысл длины диффузии (первая интерпретация): Длина диффузии в среде - это толщина слоя этой среды, в пределах которого величина плотности потока тепловых нейтронов от бесконечного плоского источника тепловых нейтронов снижается в е раз.

Можно показать также, что квадрат длины диффузии равен одной шестой среднего квадрата удаления нейтрона от точки его рождения до точки поглощения.

<L²>=<r²>/6

Это другая интерпретация физического смысла длины диффузии.

Именно такая форма распределения нейтронного поля существует в подкритических реакторах с æ_м²<0 в течение всей процедуры выхода реактора на критичность.

Вариант 2 «Размножающая среда».æ_м²>=0.

Исходное уравнение (2.10г) остается.

+ ∇ [∇ Ф(r)] +Ф(r)*1/L²{ ν_fΣ_f / K_эффΣа-1}=-Q (r)/D (2.10г)

Можно строго показать (что выходит за рамки курса), что уравнение будет иметь стационарные решения ТОЛЬКО в том случае, когда:

А.мощность нейтронного источника Q равна нулю;

Б. среда ограниченных размеров.

Тогда уравнение (2.10) приобретает вид:

ΔФ+ æ_м² Ф=0 (2.13а)

Для получения решений этого уравнения необходимо присоединить к нему граничное условие:

Ф(Rэ)=Ф(R^’)=0 (2.13.в)

Для этого рассмотрим хорошо известное в математической физике волновое уравнение Гельмгольца:

Δφ(r)+B_nφ(r)=0 (2.14а)

С граничным условием

φ(R)=0 (2.14.в)

то однородное уравнение имеет нетривиальное решение лишь при определенном наборе параметров B_n, называемых собственными числами уравнения. Их значения определяются граничными условиями.

Каждому собственному значению соответствует решение уравнения. Доказано что собственные функции уравнения Гельмгольца: ортогональны в объеме V, образуют полную систему.

Известны наборы собственных значений и собственных функций для параллелепипеда, цилиндра и сферы.

Для Параллелепипеда с ребрами a,b,c:

B²_k,l,m,= B²_x,k*B²_y,l^*B²_z,m=(kπ/a_э)²+(lπ/b_э)²+(mπ/c_э)²(2.15a)

Где k,l,m- натуральные числа;

Тогда собственные функции будут иметь вид:

φ_k,l,m (x,y,z)=cos(kπx/a_э)*cos(lπy/b_э)*cos(mπz/c_э) (2.15б).

ДляЦилиндра :

B²_k,l,= B²_r,k*B²_z,l=(kξ_к/R_э)²+ (lπ/H_э)² (2.16a).

φ_k,l (r,z)=J₀ (kξ_кr/R_э)*cos(lπz/H_э) (2.16б).

где J₀–функция Бесселя первого рода нулевого порядка;

ξ_к –к-й нуль этой функции .причем первый ξ₁ =2.405.

Для сферы:

B²_k,=B²_,k=(kπ /R_э)² (2.17a)

φ_k (r)=sin(kπr/R_э)/ (kπr/R_э) (2.17б).