Сходимость и сумма числового ряда

91) Пусть {u_n}- числ. послед.; Числовым рядом называется бесконечная сумма членов послед. u_n

т.е. u₁+u₂+…+u_n+…

ОБОЗНАЧЕНИЕ:

Суммой числового ряда называется конечный предел последоват. его частичных сумм, если существует.

ОБОЗНАЧЕНИЕ:

Запишем как: 1+1*0,2+1*

Это геометрическая прогрессия: b=1, q=0,2. Значит:

92)

т.к. ряд геометрический, то b₁=1 q-знаменатель

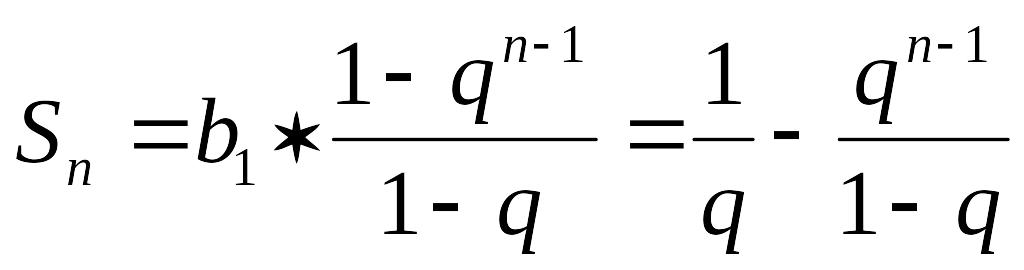
(1случай)

А) |q|<1

Б) |q|>1

(2случай) |q|=1

А) q=1

Б) q=-1

при расходится.

93) Ряд 2х сумм = сумме 2х рядов. ∑_(n=1)(a_n+b_n)= ∑_(n=1)a_n+∑_(n=1)b_n,где один расх, другой-сх. Значит, ∑_(n=1)(a_n+b_n)расх.

94) Если ряд сходится, то предел его общего члена равен нулю. (Если предел равен нулю ряд необязательно сходится, например НО он расходится.

Доказательство. Пусть данный ряд сходится и его сумма равна S. Для любого натурального n имеем , или (1)

При обе частичные суммы и

Стремятся к пределу S, поэтому из равенства (1) следует, что

Пример: В этом случае предел общего члена ряда, очевидно, равен нулю, однако ряд расходится. Действительно, если бы данный ряд сходился, то сходился бы и ряд , полученный из данного ряда группировкой членов. Но общий член последнего ряда равен 1, и для него не выполнен необходимый признак сходимости.

95)

Числ. Ряды с неотрицат. Членами

96) Для сходимости ряда необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена.

Док. Необходимость ряд a₁+a₂+a₃+…+a_n+.. – сходится. Тогда существует предел его частичных сумм. Из свойств пределов следует, что последовательность его частичных сумм ограничена.

Достаточность Поскольку все члены данного ряда положительны для любого n S_n = S_n-1+a_n то последовательность его частичных сумм монотонно возрастает. Однако известно, что ограниченная последовательность имеет предел.

97) Если для ряда с положительными членами, конечный предел

то при d >1 ряд расходится, d <1 ряд сходится.

Доказательство.

(1) d<1 т.к.

то

суммир. (k-1) нер-в

сход.

(2) d >1 т.к.

то

т.е. последовательность {u_n}возр.

ряд расходится (необ. пр.)

98) Теорема.если сущ-т предел lim_n→∞ a_n+1/a_n=d(*),то ряд сходится в случае d<1 и расх,если d>1.

Док-во: пусть d<1.возьмем некот-е число q между d и 1:d<q<1.из (*) след, что,начиная с некоторого номера n,будет выполняться нер-во a_n+1/a_n q.отсюда следует сход-ть ряда(по признаку Даламбера). случай d>1 разбирается аналогично.

При d=1 возможна как сх-ть, так и расх-ть ряда.напр, гарм.ряд, для к-го d=1, расх, а ряд 1/2²+1/3²+…+1/(n+1)²+…,для к-го также d=1,сх-ся.

По призн.Даламб.можно оценить также остаток ряда.R_n=a_n+1+a_n+2+… a_n+1+a_n+1q+a_n+1q²+…,т.е R_n a/(1-q)

Пример:1/n²,т.к…

99) Имеется ряд расходимость, которого не так очевидна.

1+1/2+1/3+1/4+1/5+….+1/n - гармонический (расход.)

Очевидно, что для гармонического ряда выполнено необходимое условие сходимости, так как (1)

Но

т.е. что противоречит (1), т.е. ряд гармонический расходится.

ЗНАКОЧЕРЕДУЮЩИЕСЯ ЧИСЛОВЫЕ РЯДЫ

100) Знакочередующиеся ряды – ряды, члены которых имеют чередующие знаки.

Теорема Лейбница Если члены знакочередующегося ряда убывают по абсолютной величине и стремяться к нулю, когда n,то 1) ряд сходится; 2) любой остаток ряда не превосходит по абсолютной величине первого из своих членов и имеет одинаковый с ним знак.

Примером условно сходящегося знакочередующегося ряда может служить ряд:

СТЕПЕННЫЕ РЯДЫ

101) Если степенной ряд сходится в точке x₁ неравной нулю, то этот ряд сходится (причем абсолютно) во всех |x|< |x₁|

а если степенной ряд расход. В точке x₂ неравной нулю, то этот ряд расходится во всех |x|< |x₂|

Ряд , сходящийся в точке х = -3, не может расходиться в точке х = 2, т.к. , следовательно согласно теореме Абеля ряд в точке х = 2 сходится, и притом абсолютно.

102) Теорема: Пусть функция f(x) разлагается на интервале (-R,R) в степенной ряд

f(x) = (1). Рассмотрим степенной ряд (2), полученный почленным дифференцированием ряда (1). Тогда:

1. ряд (2) имеет тот же радиус сходимости R, что и ряд (1);

на всем интервале (-R,R) функция f(x) имеет производную f (x), которая разлагается в степенной ряд (2)

РАЗЛОЖЕНИЕ ФУН-И В Р. ТЕЙЛОРА (МАК.)

103) Если f(x) все производные т-порядка ограничены в совокупности, т.е.

То f(x) разлагается в степенной ряд на (-R;R) т.е. ряд Маклорена сходится к своей функции.

Доказательство

При х=0 получаем

Отсюда ряд Маклорена для sinx:

104) Если f(x) все производные т-порядка ограничены в совокупности, т.е.

То f(x) разлагается в степенной ряд на (-R;R) т.е. ряд Маклорена сходится к своей функции.

Доказательство:

В любом интервале (-r;r) имеем

В силу достат. условия следует, что функция е^Х равна сумме своего ряда Маклорена при х, принадл.(-r;r), а значит, и для любого x ввиду производительности r. Поскольку f⁽ⁿ⁾(0)=e⁰=1 при любом n, получаем разложение справедливое для всех х.

105) Если функция f(x) на (-R;R) разлагается в степенной ряд , то f(x) на (-R;R) интегрируема, причем на

Найдем разложение функции f(x) = arctg x. Для этого проинтегрируем g(x)=1/1+х². Получим разложение:

arctg x=х-х³/3+х⁵/5-…+(-1)ⁿ *x²ⁿ⁺¹/2n+1+…, верное при |x|<1.

106) е^х=е+е(х-1)+е/2*(х-2)²+…+е/n!*(х-1)ⁿ+(х-1)ⁿ.

107)

КРАТНЫЕ ИНТЕГРАЛЫ.

108) Теорема: пусть для функции f(x, y) в прямоугольнике D={(x; y) | a x b; c y d} существует двойной интеграл .

Пусть, далее, для каждого х из отрезка [a, b] существует определенный интеграл

J(х)= .

Тогда существует интеграл

=

(он называется повторным) и справедливо равенство

= .

109) J(х)= .

=

=

1. =

=

110) Теорема: если преобразование – х=х(u, v) (1) – переводит область G в G* и является y=y(u,v) взаимно-однозначным и если функции (1) имеют в области G непрерывные частные производные 1-го порядка и отличный от нуля якобиан:

D (x, y) = x/ u x/ v

D(u, v) y/ u y/ v

т о при условии существования интеграла: справедлива формула замены переменных: = D(x, y)/ D(u, v) dudv.

Задача Коши

111) Если f(x,y) и f `y (x,y) заданы и непрерывны в области D<R , то ( )( ), в которой решение соотв задачи Коши ед.

Для xy`=5y – норм форма y`=5y/x (x 0)

f(x,y) = 5y/x

находим f ` y(x,y) = 5/x заданы и непр на обл D = R

Значит при сущ и ед реш-е задачи Коши

т.е. x 0

напр y(1)=2

Тогда реш-е: 2=с*1 с=2

y = cx

т.е. y = 2x - реш-е зад Коши

Заметим, что через (0,0) проходит беск много интнгр кривых, через (0,y) не прох ни одной.

Особой точкой интегральн кривой наз-ся тчк обл D, удовл одному из след услов:

1. Через нее прох беск много инт кривых

2. Не проходит ни одной интегр кривой

Особое реш-е диф ур-е это интерг кривая, полностью состоящая из особых точек.

112)

113) Частным реш-ем диф ур-я 1 пор на обл D R наз ф-я y = , которая получается из общего реш-я при конкретном c = c

114) Линейным уравнением второго порядка называется уравнение вида: y’’+P(x)y’+Q(x)y=R(x) (1), где функции P(x), Q(x), R(x) не зависят от у.

Если R(x)=0, то уравнение (1) называется однородным.

Однородное уравнение y’’+P(x)y’+Q(x)y=0 (2) обладает следующими свойствами.

Теорема 1. Если функция f₁(x) есть решение уравнения (2), то функция C₁f₁(x) (C₁ - постоянная) - также решение.

Теорема 2. Если функции f₁(x) и f₂(x) - два решения уравнения (2), то функция f₁(x)+f₂(x) - также решение.

115) Система n- функций наз линейно зависимой на мн-ве X , если хотя бы одна из них линейно выражается через остальные, напр ,

Если ни одна из них линейно н выр-ся через ост, то сист ф-ций наз. Линейно Независ

т.к.

y_1, y _2, …, y_k.

c₁ y₁+c₂ y ₂+…+ c_k y _k=0 для любого х D.

у=1, у=х, у=х² на R

c₁ 1+c₂ х+c₃ х²=0 для любого х R

Продифференцируем дважды:

c₂ +2c₃ х=0

2c₃=0

c ₁+c₂ х+c₃ х²=0 c₁=0

c₂ +2c₃ х=0 c₂=0 у=1, у=х, у=х² – л.н.з.

2c₃=0 c₃=0

116). Чтобы доказать, что эти функции л.н.з., нужно:

1. доказать, что они являются решением дифференциального уравнения;

2. проверить, что их определитель Вронского отличен от нуля.

₁=0, ₂=1, ₃=3.

( -1)( -3)=0

( ²-4 +3)=0

³-4 ²+3 =0

y^,,,-4 y^,,+3y^,=0

1 e^x e^3x e^x 3e^3x

W(1, e^x, e^3x)= 0 e^x 3e^3x = 1 e^x 9e^3x = 9e^4x-3e^4x=6e^4x 0 для любого х R.

0 e^x 9e^3x

117) Определение: система функций y₁(х)_, y ₂(х)_, …, y_n(х), состоящую из n линейно независимых решений уравнения L(y)=0, называется фундаментальный набор решений этого уравнения_.

Общее решение такого уравнения: y=C₁ y₁+ C₂ y₂+…+ C_n y_n.

118) y= e^2x, y= e^4x

y_общ.= c₁ e^2x+ c₂ e^4x

W (e^2x, e^4x)= e^2x e^4x = 2 e^6x 0 для любого х R

2e^2x 4e^4x

₁=2, ₂=4

( -2)( -4)=0

²-6 +8=0

y^,,-6y^,+8=0.

119) Определение: уравнение вида: F(n, x_n, x_n+1, x_n+2)=0, где n – произвольное натуральное число, x_n, x_n+1, x_n+2 – члены некоторой числовой последовательности, называется разностным уравнением 2-го порядка.

x_n⁽¹⁾ и x_n⁽²⁾ – решение линейного однородного разностного уравнения, их разность (x_n⁽¹⁾ - x_n⁽²⁾) – решение соответ. Однородного уравнения.

a₂(n) x_n+2+ a₁(n) x_n+1+ a₀(n) x_n=f(n) (1),

a₂(n) ,a₁(n) ,a₀(n), f(n) – извест. функции натур. аргумента, a₂(n) 0, a₀(n) 0.

a₂(n) x_n+2+ a₁(n) x_n+1+ a₀(n) x_n=0 (2).

Пусть x_n⁽¹⁾ и x_n⁽²⁾ – решения неоднородного разностного уравнения (1), т.е.

a₂(n) x_n+2⁽¹⁾+ a₁(n) x_n+1⁽¹⁾+ a₀(n) x_n⁽¹⁾= f(n) (3),

a₂(n) x_n+2⁽²⁾+ a₁(n) x_n+1⁽²⁾+ a₀(n) x_n⁽²⁾= f(n) (4).

(n)= x_n⁽¹⁾ и x_n⁽²⁾ – решение уравнения (2), если при подстановке в уравнение (2) является верным равенством.

Подставляем: a₂(n) (n+2)+a₁(n) (n+1)++ a₀(n) (n)= a₂(n)( x_n+2⁽¹⁾- x_n+2⁽²⁾)+ a₁(n) ( x_n+1⁽¹⁾-x_n+1⁽²⁾)+ a₀(n) (x_n⁽¹⁾- x_n⁽²⁾)=( a₂(n) x_n+2⁽¹⁾+ a₁(n) x_n+1⁽¹⁾ + a₀(n) x_n⁽¹⁾)-( a₂(n) x_n+2⁽²⁾+ a₁(n) x_n+1⁽²⁾ + a₀(n) x_n⁽²⁾)= f(n)- f(n)=0 (n)- решение (2).

120) Определение: уравнение вида: F(n, x_{n, …,}x_n+k)=0, где n – произвольное натуральное число, x_n, x_n+1,…, x_n+k – члены некоторой числовой последовательности, называется разностным уравнением порядка k.

2x_n+1= x_n+x_n+2 – порядок этого уравнения равен 2.

Общее решение этого уравнения: x_n=а₁+ (n-1), где а₁ и =const.

21