Скачано с сайта студентов ФА www.fa4you.ru

Предел последовательности

1) Число а называется пределом последовательности если

Обозн.

А) , Б) (-1)ⁿ

2)

Надо проверить, что для

Для нахождения n0 надо выразить n через E из неравенства

;

При этом

3) Предположим, что некоторая последовательность имеет два различных предела a и b Выберем столь маленькие окрестности точек a и b, чтобы они не имели общих точек. Поскольку , все , начиная с некоторого номера , содержится в выбранной окрестности точки а, точно также из следует, что все , начиная с некоторого номера , содержаться в некоторой окрестности точки b. Положим . Тогда числа с номерами должны принадлежать как к первой так и ко второй окрестности, что невозможно, т.к. окрестности не имеют общих точек.

4) Мн-во чисел назыв. ограниченным если сущ. такой отрезок числовой оси, который содержит все числа из Х. Док-во Пусть . Положим и найдем номер, начиная с которого для

Отсюда следует для всех . Заменим отрезок отрезком , чтобы в него попали все числа х1,х2….хn0. Тогда будем иметь для всех , что означает ограниченность мн-ва .

5) Числовая последовательность назыв. ограниченной сверху (снизу), если существует такое число М (m), что любой элемент этой последовательности удовлетворяет неравенству . Предел последовательности, ограниченной снизу числом 6 а) не может быть равным 5,98; б) может быть равным 6,02.

6) Предел суммы двух расходящихся последовательностей может сходиться. Пусть {Xn}, {Yn} – две сходящиеся последовательности, причем , , тогда . Пример расходящихся последовательностей, сумма которых сходится: 1/n; (-1)/(n+1)

7) Произведения двух сходящихся последовательностей есть сходящаяся последовательность. Предел которой равен произведению пределов соответствующих последовательностей. Пусть {Xn}, {Yn} – две сходящиеся последовательности, причем , ,

тогда . Пример расходящихся последовательностей, произведение которых сходится

{x_n}: -1, 1,-1,1……

{y_n}:-2,2, -2,2….

{x_n*y_n}: 2, 2, 2, 2….

x_n*y_n=(-1)ⁿ*(-1)ⁿ*2=2=const

lim_n→∞2=2 – сходится

8) - сходится? Если -сходится - расходится. Нет, не сходится т.к. сходящаяся последовательность {Xn}≤А, А=const. А сумма const и расходящейся последовательности расходится.

9) Последовательность называется бесконечно малой, если . а) { } и { } – бесконечно малые последовательности

lim_{n→∞ =0}

б) { } и { } – бесконечно малые последовательности

lim_n→∞ =+∞

1 0) Произведение бесконечно малой на ограниченную последовательность есть бесконечно малая. Док-во. Пусть - ограниченная, а - бесконечно малая послед. В силу ограниченности последовательности существует такое число А, что любой элемент ее удовлетворяет неравенству . Поскольку последовательность бесконечно малая, для положительного числа существует такой номер , что при всех n>N Т.о. - бесконечно малая.

11)

Допустим, что , т.е.

Допустим, что , т.е. , т.е.

12) Последовательность называется бесконечно большой, если для любого положительного числа А существует такой номер N, что при n>N (для всех элементов последовательн.) выполняется неравенств. .

При Действительно для любого положительного А существует такой номер N при что зн. последовательность является бесконечно большой. Доказательство:

Возьмем любое число A>0. Из неравенства 〡x_n〡=〡 〡>A . Если теперь взять N≥A, то для всех n>N будет выполняться неравенство 〡x_n〡>A. Так как число A может быть сколь угодно большим, то согласна определению последовательность { } будет бесконечно большой.

13) Не всякая неограниченная последовательность является бесконечно большой. Например неограниченная последовательность 1,2,1,3,1,4..,1,n.. не является бесконечно большой так как при А>1неравенство не выполняется для всех элементов с нечетными номерами.

14) Две бесконечно большие последовательности суммы которых являются бесконечно малой последовательностью. Сумма убывающей и ограниченной последовательности (1, 1/3, 1/5,…, 1/(2n-1)…) и возрастающей неограниченной последовательности (1,2,3,4,…n) является бесконечно малой последовательностью. Или пример:

15) Последовательность называется убывающей, если

Любая монотонная ограниченная последовательность имеет предел. Геометрически это означает, что если последовательность возрастает, и при этом ограничена сверху, то это означает, что с ростом n точки х_n на числовой оси смещаются вправо, но при этом не переходят через некоторый рубеж А. Геометрически ясно, что в этом случае числа x_n должны накапливаться к некоторому числу а, которое и будет пределом последовательности . Следовательно, в случае б) предела у данной последовательности просто не существует.

В случае а) предел данной последовательности больше или равен граничному члену данной последовательности.

ПРЕДЕЛ ФУНКЦИИ

16) Число а называется пределом функции f(x) в точке х₀ , если для любой сходящейся к х₀ последовательности значений аргумента, отличных от х₀, соответствующая последовательность значений функции сходится к числу а, т.е. тогда пишут

17) Предел суммы двух функций равен сумме их пределов

В силу Теоремы 1 О пределах функции где , тогда ;т.о

18) Предела ф-ции не существует т.к 1/0 нельзя

19) Число А называется пределом функции f(x) при , если для любой бесконечно большой последовательности значений аргумента, элементы которой (отрицательны) положительны соответствующая последовательность функции сходится к А. Док-во:

f(x)=cosx не имеет предела на т.е. для посл. -беск. больш. т.о. , для - беск. больш.

т.е. нет общего значения А

20) Число а называется правым (левым) пределом функции в точке а, если для любой сходящейся к а последовательности x₁, x₂, x₃,…,x_n такой, что x_n<a (x_n>a) соответствующая последовательность сходится к А.

21) 1)Если , то говорят, что является бесконечно малой более высокого порядка, чем Обознач.

2) ; ;

; при то max n=6

22)

; ; при а>2.

НЕПРЕРЫВНОСТЬ ФУНКЦИИ

23) 1)Функция f(x) называется непрерывной в точке а, если предел этой функции и ее значение в этой точке равны, т.е.

2)

в точке ; ;т.о. функция непрерывна на всей области определения т.о.а=0.

24) (Опр. Точек разрыва) Точка называется точкой разрыва f(x), если или не существует

Разрыв 1 рода если в этой точке функция имеет конечные, но не равные друг другу левый и правый пределы.

Разрыв 2 рода, если в этой точке функция f(x) не имеет по крайней мере одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.

ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ

25) (Теорема о существовании нуля) Пусть функция f(x) непрерывна на отрезке [a;b] и на его концах принимает значение разных знаков. Тогда внутри [a;b] существует точка c, в которой f(x)=0

Вопр. Производной функции у=f(x) в точке x0 называется предел отношения , когда (при условии, что предел отношения существует)

26-31) Опр. Пусть ф-ция определена в некоторой окрестности точки (∆ = ). Производной ф-ции в точке называется предел отношения , когда (при условии, что предел отношения существует). Обозначение .

31) Решение.

32) Если z=f(x;y) дифференцируема в точке (х₀;y₀), то в этой точке она непрерывна.

Пусть ф-ция z=f(x;y) дифференцируема в точке (х₀;y₀), тогда справедливо

ф-ция z=f(x) непрерывна в точке (х₀;y₀).

33) Если f(x) дифференцируема в т. x0 то f(x) непрерывна в этой точке. Обратное неверно: например - непрерывна, но не является дифференцируемой.

34) Теорема Если функции u=f(x), v=g(x) дифференцируемы в точке x₀, то сумма, разность, произведение и частное этих функций (частное при условии g(x) не равно 0) также дифференцируемы в точке x₀, и выполняются следующие формулы:

Пусть приращения функций u, v, u+v, uv, u/v, вычисляются только в точке x₀, так, что:

И так далее, как видно, приращение суммы d(u+v) равно сумме приращений du+dv. Действительно, d(u+v)= (u+du)+(v+dv)-(u+v)= du+dv. Аналогично с минусом. Поэтому:

35) 1)(Производная обратной функции) Пусть функция y=f(x) является непрерывной и строго монотонной в некоторой окрестности точки x₀ и имеет в этой точке производную . Тогда обратная функции также имеет в соответствующей точке производную, причем:

2)

Вопр. ОПР Функция y=f(x) называется дифференцируемой в точке x₀, если ее приращение в точке x₀ можно представить в виде

, где А- некоторое число - функция от являющаяся бесконечно малой, при .

Прим.

36) Дифференциалом функции в точке х₀ называется линейная относительно приращения аргумента часть приращения функции в этой точке, эквивалентная всему приращению.

df(х₀)= f ′ (х₀) ∆х; ∆х=dх; df(х₀)= f ′ (х₀) dх

37) см. вопрос 36 +

ЭЛАСТИЧНОСТЬ

38) Эластичностью фун-ции в т. назыв. предел: Эластичность E_y – это коэффициент пропорциональности между относительными изменениями величин у и x.

39) см. вопрос 38.+

1.

40) Эластичность произведения функций u=u(x) и v=v(x) в точке равна сумме эластичностей функций u и v в той же точке:

По формуле получим

Аналогично доказывается для эластичности частного.

ЛОКАЛЬНЫЙ ЭКСТРЕМУМ

41) Точка x₀ называется точкой локального максимума (соответственно локального минимума) функции f(x), если для все х из некоторой окрестности точки x₀ выполняется неравенство (соответств. )

Необходимое условие: Для того, чтобы дифференцируемая функция f(x) имела в точке x₀ локальный экстремум, необходимо, чтобы в этой точке выполнялось равенство .

Т. в которых производная обращается в ноль – стационарные т.

Функция f(x)=x³ . Эта функция возрастает на всей числовой прямой и, поэтому не имеет точек локального экстремума. Но т. x₀ =0 явл. Стац точкой т.к.

ТЕОРЕМЫ РОЛЛЯ, ЛАГРАНЖА, КОШИ

42) (Теорема Ролля) Пусть ф-ция f(x) непрерывна на отрезке [a;b], дифференцируема на интервале (a;b), и f(a)=f(b), тогда существует точка в которой . заданному интервалу принадлежит только 1 точка.

43) Пусть функция f(x) непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда существует такая точка , что - формула конечных приращений.

44) Пусть ф-ция непрерывна на отрезке [a;b], дифференцируема на интервале (a;b), то существует точка такая, что .

возрастает.

45) Пусть функции f(x) и g(x) непрерывны на отрезке [a;b] и дифференцируемы на интервале (a;b). Пусть кроме того, на (a;b). Тогда существует точка , т., что

2)По теореме о конечных приращениях

ФОРМУЛА ТЕЙЛОРА (МАКЛОРЕНА)

46) Пусть ф-ция имеет производных в точке . Многочлен называется n-многочленом Тейлора функции в точке .

аналогично . И так далее.

Составим многочлен Тейлора 3его порядка с центром в точке

47)

48)

ПРОСТРАНСТВО R²

49) Пусть . Расстоянием между X и Y называется число . Расстояние между точками, определённое этой формулой, задаёт отображение и удовлетворяет следующим свойствам:

1. если

2. 

3. 

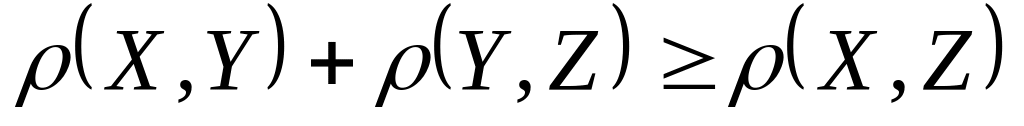
Доказательство 1 и 2 очевидно. Докажем 3. Заметим, что пара точек определяет вектор .

Проведём серию равносильных преобразований

5 0) Множество D называется открытым если все его точки внутренние. D- прямоугольник OABC с исключенными AB и OC. Данное множество не является открытым, т.к. точки отражающие OA BC являются граничными, а не внутренними.

51) Множество D называется замкнутым, если оно содержит все свои граничные точки. D- прямоугольник OABC с исключенными AB и OC. Данное множество не является замкнутым, т.к. граничные точки из отрезка AB и ОС исключены из множества.

52) Т. М₀ называется предельной точкой мн-ва D, если в любой есть точки из множества D.

А)

D

Б) является предельной, но множеству D не принадлежит.

СХОДИМОСТЬ ПОСЛЕДОВАТЕЛЬНОСТИ

53) Последовательность точек евклидового пространства E^m называется сходящейся, если существует такая точка А, что для любого числа можно указать номер N, начиная с которого (при n>N) все точки этой последовательности будут находиться в - окрестности точки А, т.е. .

последовательность сходится к точке (1,1)

ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ

54) Число а называется пределом ф-ции f(M) в т. A _, если для любого числа можно найти такое число , что для всех точек точки А (удовлетворяющих неравенству выполняется неравенство . по теореме о произведении бесконечно малой на ограниченную ф-ции.

55) Функция не имеет предела в точке (0;0).

56) Ф-ция u=f(M) называется непрерывной в точке А, если предел функции в этой точке существует и равен значению ф-ции в этой точке. .

ЧАСТНЫЕ ПРОИЗВОДНЫЕ, ДИФФЕРЕНЦИАЛ

57) Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения частного приращения функции к приращению соответствующей независимой переменной, когда это приращение стремиться к нулю.

58) Функция z=f(x;y) называется дифференцируемой в точке (x₀,y₀), если ее полное приращение можно представить в виде

Если функция дифференцируема в точке, то она непрерывна в этой точке.

Необходимо проверить , что когда . Проверим вычислением:

ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ (GRAD)

59) Градиент ф-ции в точке М называется вектор координаты которого равны соответствующим частным производным данной функции в точке М. Так для ф-ции двух переменных f(x,y) имеем т.о. используя формулу вычисления производной дифференцируемой функции z=f(x,y) в точке (x₀;y₀) в направлении e: получим формулу: , где - скалярное произведение векторов.

60) Градиентом ф-ции z= f(x,y) в точке M(x,y) называется вектор, координаты которого равны соответствующим частным производным , взятым в точке M(x,y).

По определению скалярного произведения . Учитывая, что . Из последнего следует, что производная по направлению имеет наибольшую величину при , то есть когда направление вектора совпадает с направлением .

ОДНОРОДНЫЕ ФУНКЦИИ

61) Функция определенная на множестве {М}, называется однородной функцией степени на этом множестве, если для любой точки М(x₁;x₂;…x_m) этого множества и для каждого числа t, для которого точка N (tx₁;tx₂…tx_m) также принадлежит {М}, выполняется равенство

62) Пусть D из Rⁿ – область в Rⁿ, содержащая с каждой своей точкой (x₁, x₂, …., x_n) и все точки вида (tx₁, tx₂, …., tx_n) при t>0 функция f(x₁, x₂, …., x_n) с такой областью определения D называется однородной степени λ, если для любого t>0 выполнятся равенство f (tx₁, tx₂, …., tx_n)=t^λ f(x₁, x₂, …., x_n).

Пример однородной функции степени 3:

F (x,y)=x²

F (tx, ty)=t²x²√(tx*ty)=t³ F (x,y)

63) Док-ть:

Предположим, что дифференцируемая функция f(x,y) является одновременно и однородной функцией степени . Фиксируя произвольную точку (x,y), для любого t>0 имеем Продифференцируем левую и правую части этого равенства по t, тогда получим: Предположив t=1, получим формулу Эйлера:

ЛОКАЛЬНЫЙ ЭКСТРЕМУМ

64 1)Точка называется точкой локального максимума (минимума) ф-ции ,если существует такая -окрестность, точки в которой для любой точки - выполняется неравенство

2) Для того, чтобы дифференцируемая ф-ция имела локальный экстремум в точке , необходимо, чтобы все ее частные производные первого порядка в этой точке были равны 0.

65)1)для того чтобы дифференцируемая функция имела локальный экстремум в точке а, необходимо, чтобы все ее частные производные первого порядка в этой точке были равны 0.

f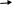 ’_x=2xy⁴ 2xy⁴=0

f ’_y=4x²y³ 4x²y³=0

Подставим координаты точки в оба уравнения и получим два верных равенства. Значит, данная точка является стационарной, то есть точкой “подозрительной” на экстремум.

2 ) для того чтобы дифференцируемая функция имела локальный экстремум в точке а, необходимо, чтобы определитель вида f’’_xx f’’_xy был больше 0.

f’’_xy f’’_yy

f ’’_xx=2y⁴ 2y⁴ 8xy³ =0

f’’_yy=12x²y² 8xy³ 12x²y²

f’’_xy=8xy³

Определитель равен 0, однако поскольку для всех значений (x,y) f(x,y)>f(0,0), то данная точка является глобальным экстремумом, а значит, является и локальным экстремумом.

66) Имеет ли функция f(x,y)=x²+y² локальный экстремум в точке (0 , 0) ?

1 )f’_x=2x 2x=0 верно, значит данная точка является стационарной

f’_y=2y 2y=0

2) f’’_xx=2 2 0 =4-0=4>0, значит (0,0) - точка локального экстремума, f’’_xx>0, значит точка

f’’_yy=2 0 2 локального min

f’’_xy=0

67) Докажите, что функция f(x,y)=x²+y²: а) не имеет локального

экстремума в точке (1 , 1) , б) имеет в этой точке условный локальный

экстремум при наличии связи x+y=2.

а)найдем частные производные первого порядка

f ’_x=2x 2x=0, координаты данной точки не являются решениями данных уравнений,

f ’_y=2y 2y=0 значит (1,1) не является точкой локального экстремума.

б) применим метод множителей Лагранжа, получим f(x,y)=x²+y²+λ(x+y-2), найдем частные производные первого порядка

f ’_x=2x+λ 2x+λ=0 x=y

f ’_y=2y+λ 2y+λ=0 x=1

f ’_λ=x+y-2 x+y-2=0 y=1

f ’’_xx=2 2 0 =4>0, значит точка локального экстремума, f’’_xx>2, значит точка локального

f’’_yy=2 0 2 min

f’’_xy=0