2.1.2 Прикладные задачи в табличном процессоре Excel

Задача 1: Работа с формулами и ссылками

Продукцией городского молочного завода являются молоко, кефир и сметана. На производство 1т молока, кефира и сметаны требуется соответственно 1010, 1020 и 9450 кг молока.

Прибыль от реализации 1т молока, кефира и сметаны соответственно равны 3000, 2200 и 1360 руб. Было изготовлено молока 123 т, кефира 342 т, сметаны 256т.

Задание:

а)при помощи электронной таблицы рассчитать:

-расход молока (сырья),

-прибыль от реализации каждого вида изделий,

-общую прибыль,

-долю (в процентах) прибыльности каждого вида изделий от общей суммы;

б) построить диаграммы по «расходу сырья для каждого вида изделия» и « прибыль от реализации каждого вида изделий».

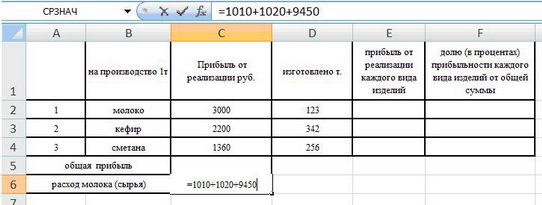
Создать таблицу, изображённую на рисунке. Произвести все расчёты и заполнить все ячейки значениями.

Контрольные вопросы:

1. Назначение и возможности табличного процессора Excel.

2. Как создать новое окно документа в Excel?

3. Какие величины могут быть помещены в ячейки таблицы Excel?

4. Какая ячейка называется активной?

5. Как ввести и редактировать данные в Excel?

6. Как применяется функция Автосумма?

Задача 2: линейная оптимизация производства

Предприятие выпускает 3 вида изделий. Для выпуска единицы изделия необходимо сырье в количестве 3 кг для 1-го вида, 8 кг для 2-го вида и 1 кг для 3-го вида. Общий запас сырья составляет 9500 кг. Изделия по видам входят в комплект в количестве 2, 1 и 5 штук соответственно. Определить оптимальное количество выпуска изделий, при котором количество комплектов будет максимальным. Комплекты немедленно отправляются потребителю. Склад вмещает не более 20 штук лишних изделий 2-го вида.

Решение:

Пусть х – количество комплектов,

тогда 2*х – количество изделий вида1,

х – количество изделий вида2,

5*х – количество изделий вида3.

Целевая функция: х ->max.

Ограничение по сырью: 3*2*х+8*х+3*5*х≤9500

х1>=1,

х2>=1,

х3>=1.

Для решения задачи в Excel запишем ее в виде, представленном на рисунке:

В ячейку В3 введем формулу: =B2*2

В ячейку В4 введем формулу: =B2

В ячейку В5 введем формулу: =B2*5

В ячейку C6 введем формулу: =3*B3+8*B4+B5

В ячейку D7 введем формулу: =B2

Выберем команду Сервис-> Поиск решения. Введем параметры:

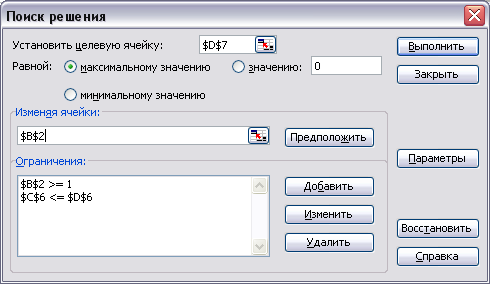
Нажмем кнопку Выполнить.

После нажатия кнопки ОК получим:

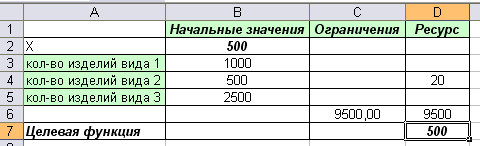
Ответ: предприятию следует выпускать в день 1000 изделий 1-го типа, 500 изделий 2-го типа и 2500 изделий 3-го типа, тогда количество комплектов будет максимально и равно 500 штук.

Задача 3: линейная оптимизация транспорта

Груз, хранящийся на двух складах (A и B) и требующий для перевозки 20 и 30 автомашин соответственно, необходимо перевезти в три магазина. Первому магазину требуется 10 машины груза, второму – 30 и третьему – 10. Стоимости перевозки одной автомашины указаны в следующей таблице:

Склады	Магазины
	1	2	3
A	4	9	3
B	4	8	1

Требуется составить оптимальный по стоимости план перевозки груза от складов до магазинов.

Решение задачи

1.Подготовка задачи к решению

Пусть x_ij количество автомашин перевезенных из пунктов (склады А и В) отправления в пункты назначения (магазины 1, 2 и 3);

Тогда система ограничений и целевая функция(транспортные расходы) запишутся следующим образом:

4x₁₁ + 9х₁₂ + 3х₁₃ +4х₂₁+8 х₂₂+x₂₃ min (целевая функция );

x11 + х21 =10		Все потребности магазинов должны быть удовлетворены
x12 + х22=30
x13 + х23=10
x11 + х12 + х13 =20		Все запасы должны быть исчерпаны
X21 + х22 + х23 =30

2.Подготовка рабочей книги.

Для решения задачи в Excel запишем ее в виде, представленном на рис. 1.

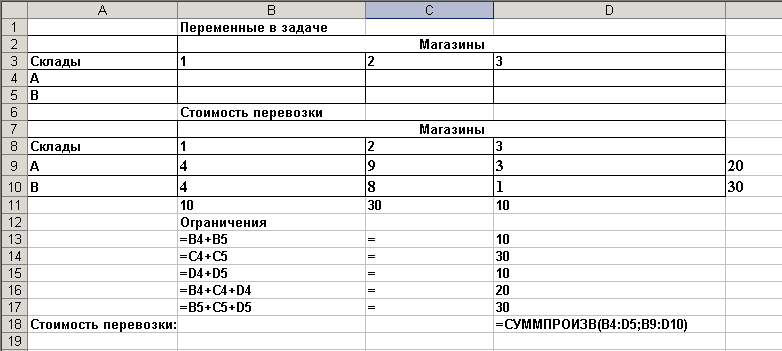
Рисунок 1 – Вид рабочего листа Excel

Далее вызываем Поиск решения из меню Сервис.

Определяем целевую ячейку (в нашем случае D18), устанавливаем переключатель в минимальное значение. Вводим диапазон изменяемых ячеек ($B$4:$D$5) и вносим ограничения.

Прежде всего, количество перевозимого груза не может быть отрицательным ($B$4:$D$5$>= 0), далее добавляем ограничения на потребности и запасы груза, которые должно быть равны требуемым (В$13=D$13), и т.д. по всем ограничениям.

Нажимаем кнопку Выполнить и получаем следующий оптимальный план перевозки груза, представленный в таблице.

Склады	Магазины
	1	2	3
A	10	10	0
B	0	20	10

Задача 4: табулирование функции

Тривиальные задачи на табулирование функции представляют из себя прикладные математические исследования. При решении такого рода задач требуется задать определенные ограничения. Разберем пример.

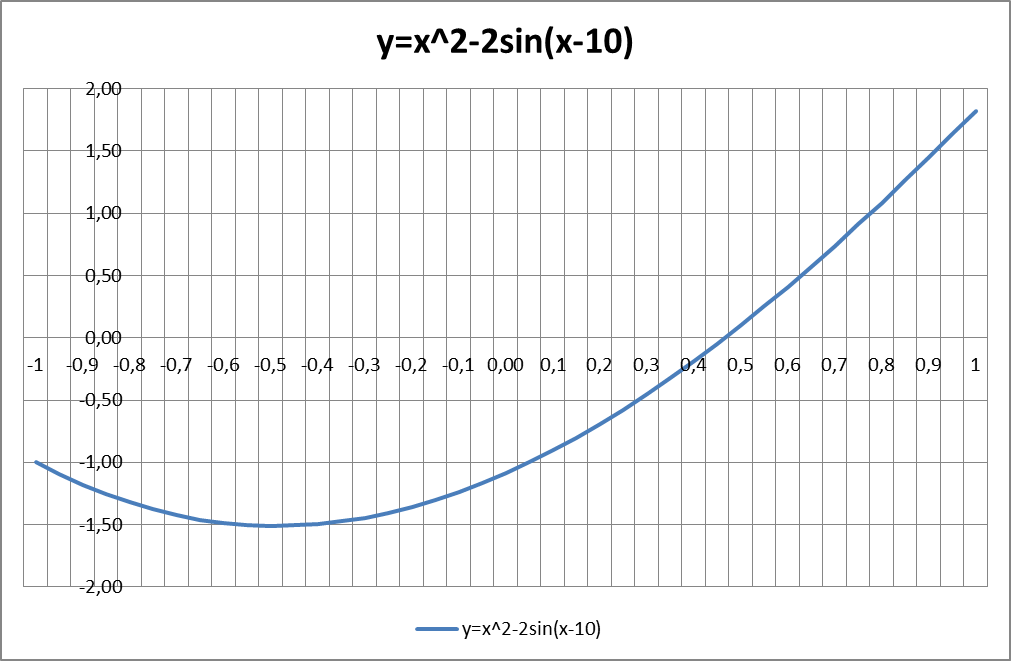
Задача: Построить график функции и найти корни уравнения y=x²-2sin(x-10) на отрезке [-1;1] с шагом 0,05.

Работа на компьютере проводится в среде MS Excel с применением динамических и статических ссылок.

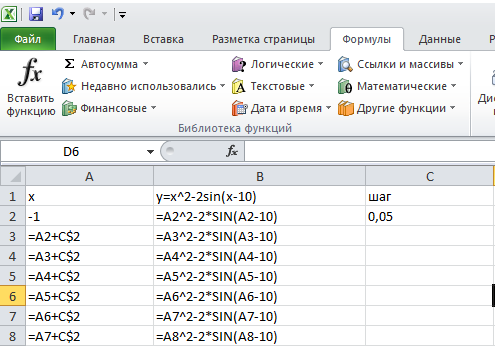
Сначала заполняется таблица с данными. В ячейках А1-С1 заголовки, в ячейке А2 – начальное значение заданного диапазона [-1;1], в ячейке В2 – формула для расчета заданной функции y=x²-2sin(x-10), в ячейке С2 – заданный шаг, для использования которого требуется употребить абсолютные ссылки.

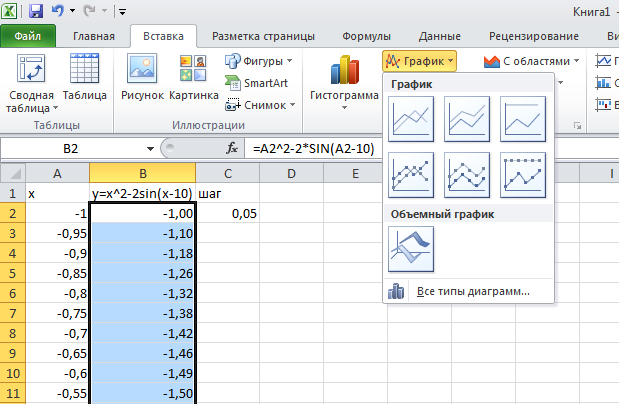
Для построения графика необходимо выделить диапазон данных (ячейки В2:В42), в меню выбрать закладку «Вставка», выбрать на панели инструментов «График», и вставить соответствующий график функции. Для получения отличного результата нужно правильно оформить график функции: разместить оси координат с пересечением в точке 0;0, отобразить основные линии сетки для приближенного вычисления корней уравнения.

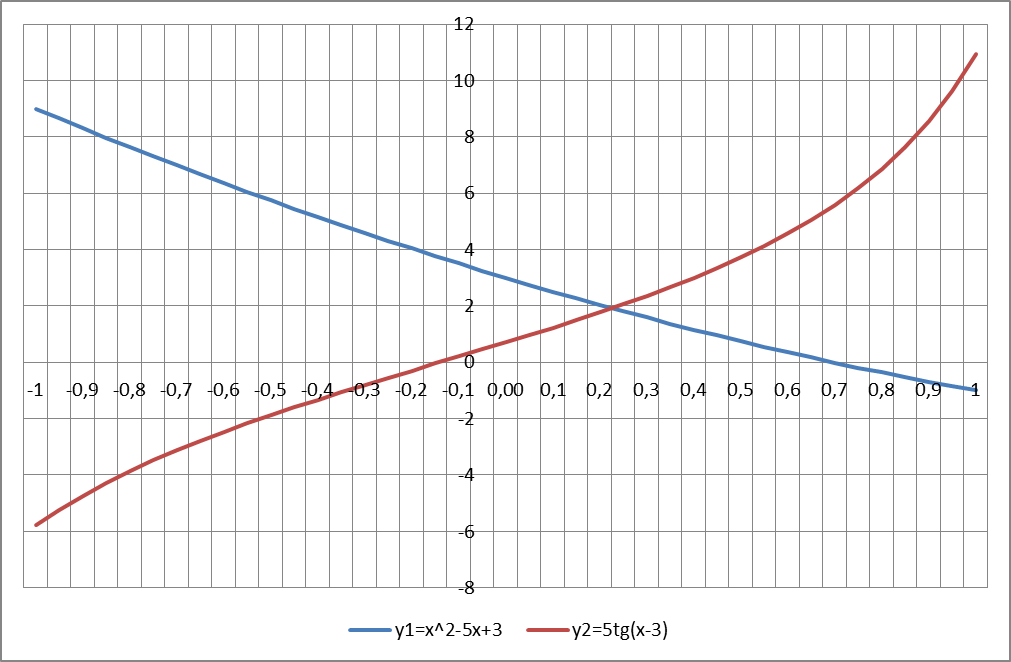
Задача 5: Приближенное решение системы уравнений

Задача: Найти приближенное решение системы уравнений графическим методом.

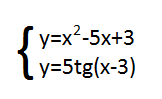
Сначала заполняется таблица с данными. В ячейках А1-С2 заголовки, в ячейке А2 – начальное значение заданного диапазона [-1;1], в ячейке В2 – формула для расчета первого уравнения y=x²-5x+3, в ячейке С2 – формула для расчета второго уравнения y=5tg(x-3), в ячейке D2 - заданный шаг, для использования которого требуется употребить абсолютные ссылки.

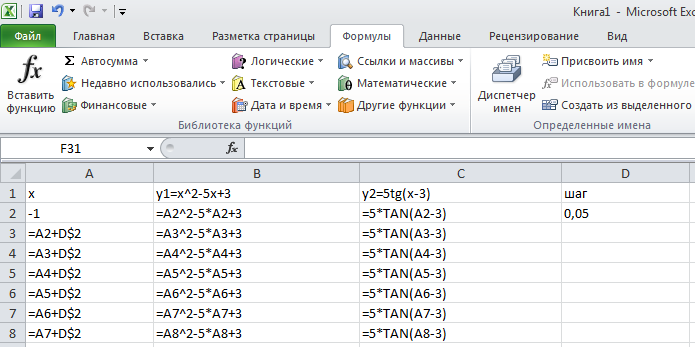
Для построения графика необходимо выделить диапазон данных (ячейки В2:С42), в меню выбрать закладку «Вставка», выбрать на панели инструментов «График», и вставить соответствующие графики функций. Для получения отличного результата нужно правильно оформить решение системы уравнений: разместить оси координат с пересечением в точке 0;0