16. Энергия заряженного проводника. Энергия электрического поля.

Заряд проводника образуется точечными зарядами qi. Они находятся в эл.поле, потенциал которого равен фиi. Энергия системы этих зарядов W=1/2*

W=q*φ/2=C*φ^2/2=q^2/2C

Для конденсатора энергия состоит из суммы энергий положительной и отрицательной пластин

W= q*φ+/2+ (-q)*φ-/2=q*U/2

Для плоского конденсатора C=ε*ε0*S/d. Т.к. U=E*d, то W=C*U^2/2= ε*ε0*S*E²*d² / (2*d)= ε*ε0*E² /2 * S*d, где S*d=V – энергия поля

Получили выражение для W, не содержащее заряда, а только напряжённость поля, полученное выражение для W дат энергию эл.поля, возникшего между обкладками конденсатора в результате зарядки.

Плотность энергии эл.поля ω=ε*ε0*E² / 2 = (E(),D())/2

Энергия заряженного конденсатора сосредоточена в его электрическом поле.

17.Электрический ток. Уравнение непрерывности.

Электрический ток — это упорядоченное движение заряженных частиц в проводнике. Чтобы он возник, следует предварительно создать электрическое поле, под действием которого вышеупомянутые заряженные частицы придут в движение.

Для существования эл тока необходимо 1)Наличие носителей тока (зарядов, способных перемещаться по объёму тела) 2)Ненулевое поле внутри проводника

Кол-венная хар-ка эл.тока – сила тока – заряд, переносимый через выбранную поверхность в ед времени I= dq/dt

J – вектор плотности тока. По модулю равен силе тока через элементарную площадку dS, перпендикулярную направлению движения носителей тока делить на величину этой площади, т.е. j=dI/dS Направление совпадает с напралением вектора скорости упорядоченного движения положительных носителей тока . Сила тока является потоком вектора плотности тока. Если пов-сть S замкнута, то эта величина даст убыль заряда внутри охваченного S объёма в единицу времени. Можно написать: Получим ур-ие непрерывности для тока. Оно отражает закон сохранения заряда. Левую сторону ур-ия перепишем, воспользовавшись т.Остр-Гаусса: =-d/dt * = dV. В силу произвольности выбора пов-сти S и V следует положить равенство подынтегральных выражения (набла, j)=- . Если токи стационарны, т.е. не зависят от времени, то =0 divj=0.

Пусть в проводнике сущ. носители тока е+ и е-. Перенос зарядов через S происходит в противоположном движении, т.е. . Условно можно считать, что происходит движение зарядов –е- со скоростью - , поэтому сила тока определяется, как I=dq+/dt + |dq-|/dt. Запишем j через скорость и концентрацию: РИСУНОК

За время dt через dS_|_ пройдут все положительные носители тока, находящиеся в выделенном цилиндре. Заряд, прошедший через dS_|_, dq+=e+*dN+=e+*n+*(U+)dt*dS_|_ , где n+ - концентрация положительных носителей тока|j+|=dq+/(dt*dS_|_)=e+*n+*U+=ρ+*U+. Итак, = (e+*n+*U+)+ e-*n-*U-

18-19. ЭДС. ЗАКОНЫ ОМА

Для существования тока в проводнике необходимо наличие ненулевого эл.поля. Оно создаётся за счёт некоторого распределения заряда вследствие движения положит.носителей из точек с большим потенциалом в точки с меньшим. Поле быстро исчезает, и ток прекращается. Для его поддержания необходимо существование сил неэлектростатического происхождения, которые переносили бы положительные носители из точек с меньшим φв точки с большим. РИСУНОК

Эти силы называют сторонними, т.к. они имеют эл/магн природу, так же они пропорциональны переносимому заряду. =q* . Количественной характеристикой их является совершаемая ими работа на некотором участке цепи, отнесённая к величине переносимого заряда – ЭДС

ЭДС1,2 = Астор/q =

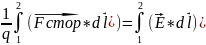
Электродвижущая сила (ЭДС) — физическая величина, характеризующая работу сторонних сил в источниках постоянного или переменного тока.

На участке цепи действует сила =q* +q* . Она характ. падением напряжения U12= = )+ . Итак, U12=φ1-φ2+ε12. Для замкнутой цепи U=ε. Для однородных металлич. проводников в отсутствие магн.поля выполняется Закон Ома I=U/R=G*U. Если проводник цилиндрический, то R=ρ*l/S, σ=1/ρ- удельная проводимость. Выделим в проводнике цилиндр объём dl*dS_|_, образующие которого || . РИСУНОК

I= *dS_|_; U= φ1-φ2=E*dl; R= ρ*dl/dS_|_; j*dS_|_=E*dl/(ρ*dl) *dS_|_--> j=E/ ρ=σ* – закон Ома в дифф.форме.

Если действуют сторонние силы, то следует написать: заряды движ. за счёт эл.поля и стор.сил: =(1/ρ)*( + |*dl скалярно, j=I/S_|_ |  = ( + ; dl =  I*R=U12= φ1-φ2+ ε12 – закон Ома для неоднородного участка цепи. Для замкнутой цепи I*R= ε, φ1=φ2.

Пусть по цепи протекает постоянный ток I, за время t переносится заряд q=I*t на некотором участке цепи 1-2, силы эл/стат поля и сторонние совершают работу А12=q*U12=I*U12*t, называемая работой тока. Мощность P=I*U12. Эта работа идёт на увеличение внутренней энергии проводника, хим.реакции, на работу по перемещению проводника. Если проводник однороден и неподвижен, то вся работа тока идёт на нагревание. Согласно экспериментальному закону, количество теплоты, выделяющейся при прохождении тока, =I^2*R*t – закон Джоуля-Ленца. В случае однородного неподвижного проводника выполняется закон Ома. Для небольшого цилиндрического проводника I=j*dS_|_ , R=ρ*dl/dS_|_ , Q=j^2*(dS_|_)^2* ρ*dl/ (dS_|_)= ρ* j^2*dV*t. Удельная тепловая мощность Q= ρ* j^2