5. Диполь. Поле диполя.

Электрическим диполем называется система двух одинаковых по величине разноимённых точечных зарядов +q и –q, на расстоянии l между которыми значительно меньше расстояния до тех точек, в которых определяется поля системы. Прямая, проходящая через оба заряда, называется осью диполя.

Поле диполя обладает осевой симметрией. Поэтому вид поля в любой плоскости, проходящей через ось диполя, будет одной и той же, причём вектор E лежит в этой плоскости.

С учетом неравенства сможем записать

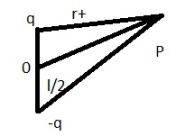
Потенциал эл.поля, создаваемого диполем в точке Электрический дипольный момент . Напряженность поля определим по проекциям на направление задаваемое изменением R:

6. Диполь во внешнем электрическом поле

Сначала — в однородное поле с напряженностью  E⃗  (рис. 3).

На заряды диполя действуют равные по модулю, но противоположные по направлению силы  +qE⃗  и  −qE⃗ , которые стремятся развернуть диполь. Относительно оси, проходящей через центр диполя (точку О) и перпендикулярной плоскости чертежа, каждая сила создает вращающий момент, равный произведению модуля силы на соответствующее плечо (см. рис. 3)

 qE⋅l2sinα

Суммарный вращающий момент будет равен

 M=2qE⋅l2sinα=qlEsinα=p⋅Esinα .

Таким образом, при заданных значениях Е и α вращающий момент М определяется величиной дипольного момента р.

Под действием вращающего момента диполь будет поворачиваться, пока не займет положение, изображенное на рисунке 3 штриховой линией. В этом положении равны нулю как сумма сил, так и сумма моментов сил, действующих на диполь. Это означает, что диполь находится в равновесии. При этом вектор электрического момента диполя сонаправлен с вектором напряженности поля. Следовательно, в однородном внешнем электрическом поле диполь поворачивается и располагается так, чтобы его дипольный момент был ориентирован по полю. Заметим, что такое положение является положением его устойчивого равновесия.

Пусть теперь диполь находится в неоднородном внешнем поле. Разумеется, и здесь возникает вращающий момент, разворачивающий диполь вдоль поля (рис. 4). Но в этом случае на заряды действуют неодинаковые но модулю силы, равнодействующая которых отлична от нуля. Поэтому диполь будет еще и перемещаться поступательно, втягиваясь в область более сильного поля

7. Градиент.Дивергенция.Ротор.

1)градиент

Пусть задано скалярное поле ф(r)=ф(x,y,z). Рассмотрим приращение скалярного поля dф при перемещении dl=dxi+dyj+dzk от точки, радиус-вектор которой r,(r+dl)

Тогда Градиент скалярной функции позволяет найти ее приращение при перемещении dl

2)дивергенция:Под потоком понимают объем жидкости протекающей через некотор выделенную поверхность в 1 времени.Отличие потока от нуля через замкнутую поверхность означает наличие источников или стоков жидкости. Величина Ф определяет суммарную алгебраическую мощность источников в объем V. -средняя мощность источников.При V  0 — удельная мощность точки P ,ее называют дивергенцией (расхождением) вектора : Интеграл берется по любой замкнутой поверхности, содержащей точку V.В декартовых координатах, ;

3) ротор :Аддитивность циркуляции позволяет ввести понятие удельной циркуляции, т.е. отношение с к величине поверхности S.При конечных размерах S отношение с/S дает среднее значение удельной циркуляции.В точке поле будет характеризовать выражение: где с – циркуляция вектора по контуру Г, S – площадь контура. В одной и той же точке Р для разных будем получать различные значения. Максимальные величины дает модуль вектора, а его направление по , когда максимально.Этот вектор называется ротором . ;;