31.Уравнение максвелла

Открытие тока смещения позволило Максвеллу создать единую теорию электрических и магнитных явлений. Основу электромагнитной теории света максвелла образуют уравнения максвелла. Первая пара уравнений максвелла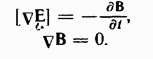 первое уравнение связывает значение Е с изменениями вектора В во времени и является по существу выражением закона электромагнитной индукции. Второе уравнение указывает на отсутствие источников магнитного поля, т.е. магнитных зарядов. 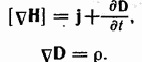Вторая пара уравнений первое устанавливает связь между токами проводимости и смещения и порождаемым ими магнитным полем. Уравнения максвелла в скалярной форме

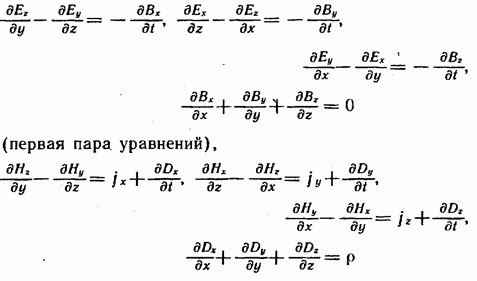
32.Волновое уравнение для электромагнитного поля

Существование электромагнитных волн вытекает из уравнений максвелла. В случае однородной нейтральной непроводящей среды с постоянными проницаемостями µ и ɛ

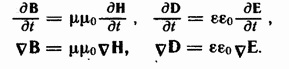
Поэтому уравнения максвелла можно записать следующим образом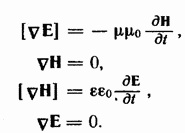 Из этих уравнений можно составить уравнение 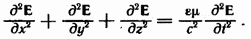Взяв ротор от обейх частей этого уравнения придем к уравнению 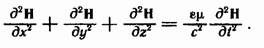уравнения получены из первого и третьего уравнений максвелла. Составленные уравнения представляют собой типичные волновые уравнения. Всякая функция, удовлетворяющая такому уравнению, описывает некоторую волну. Они указывают на то, что электромагнитные поля могу сущетсвовать в виде электромагнитных волн, фазовая скорость которых равна

33. Плоская электромагнитная волна

Волна называется плоской, если поверхности равных фаз представляют собой плоскость, т.е. в плоской электромагнитной волне векторы   и   расположены в плоскости хода, перпендикулярно направлению распространения волны.

Однородной плоской волной называется волна, в которой при соответствующем выборе осей координат векторы   и   зависят только от одной координаты и времени 

Если векторы   и   изменяются по синусоидальному закону, то волна называется гармонической или монохроматической.

По определению плоской волны

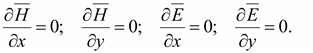
В плоской волне   и   являются функциями только одной координаты – z. Из системы уравнений (18.12) для синусоидальных функций в комплексной форме записи получается:

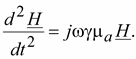
Решение линейного дифференциального уравнения второго порядка имеет вид

34. Энергия и импульс электромагнитной волны.

ЭМ волна обладает энергией, которая в результате волнового процесса переносится в пространстве. Энергия ЭМ волны это энергия эл и магн полей.

Для плотности энергии , где H – напряжённость магнитного поля.

, где V – скорость волны.

E и H меняются со временем => плотность энергии в выбр точке будет меняться от wmin=0 до . Таким образом энергия распространяется в пространстве. Для кол-венной хар-ки направления и интенсивности используется вектор плотности потока энергии, который направлен в сторону распространения волны. Его модуль равен энергии, переносимой в ед времени, через ед. площадку перпендикулярную

Вектор плотности потока энергии

Полученный вектор называют вектором Поинтинга.

Зная вектор поинтинга можно вычислить поток энергии через произвольную поверхность.

При прохождении эм волны через некоторое тело, она оказывает на него силовое воздействие : вектор E заставляет электроны проводимости двигаться, возникает эл ток, плотность которого сигмаE, действует сила Лоренца, которая и есть воздействие на тело, эта сила вызывает изменение импульса тела => волна обладает импульсом.