1. Электрический заряд. Закон кулона.

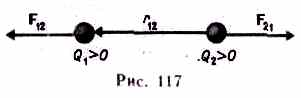
Электрический заряд характеризует способность тел к электромагнитному взаимодействию. Св-ва эл.заряда. 1) одноименные заряды отталкиваются, разноименные притягиваются. 2)все тела состоят из элементарных частиц(электроны, протоны, нейтроны) (e= 1,6*10^-19 Кл) , следовательно заряд любого тела кратен элемен.заряду е. q=Ne;N=0,1,2… 3) электрический заряд тела независит от скорости движения тела 4)выполняется закон сохранения эл.заряда: заряд электроизолированной системы не меняется со временем. Точечным на­зывается заряд, сосредоточенный на теле, линейные размеры которого пренебрежимо малы по сравнению с расстоянием до дру­гих заряженных тел, с которыми он взаи­модействует.

З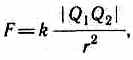 акон Кулона: сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, про­порциональна зарядам Q₁ и Q₂ и обратно пропорциональна квадрату расстояния r между ними:

В СИ коэффициент пропорционально­сти равен k=1/(4₀). Тогда закон Кулона запишется в оконча­тельном виде: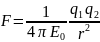 Величина ₀ называется электрической постоянной ₀=8,85•10^-12Кл²/(Н•м²), Для закона Кулона выполняется принцип суперпозиции: сила, с которой некотороя система зарядов q1,q2…qn действует на заряд q0 равна векторной сумме сил с которыми действуют заряды q1..qn на q0 взятые поотдельности.

2.Напряженность поля. Потенциал.

Взаимодействие между неподвижными зарядами осуществляется посредством электрического поля. Заряды создают в окруж. Пространстве эл.полеб которое обнаруживается по его воздействию на другие заряды. Количественными характеристиками эл.поля являются векторная величина напряженность Е(1В/м) и сколярная величина потелниал ф(1В). Пусть эл.поле создает система зарядов q1,q2…qn. Сила, с которой эта система действует на пробный заряд q0 равна

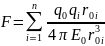
E-силовая хар-тика эл.поля, зная Е можно найти силу, действующую на заряд, помещенный в это поле. Для напряженности выполняется принцип суперпозиции: напряженность поля системы зарядов равна векторной сумме напряженностей полей создаваемых каждым зарядом взятым поотдельности. Выражения длс напряженности точечного заряда ( ) и принцип суперпозиции позволяют вычислить напряженность системы зарядов. Работа, совершаемая силами эл.поля создаваемого неподвижным точечным зарядом может быть представлена как убыль потенциальной энергии заряда q0

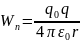
Потенциал – энерг.характеристика поля, т.к. зная его можно найти потенциальную энергию точечного заряда q (W=qф) Любая работа, которая будет совершаться полем, будет происходить за счет уменьшения потенциальной энергии.

В случае если поле создается несколькими зарядами, которые расположены в произвольном порядке. Потенциал в данной точке такого поля будет представлять собой алгебраическую сумму всех потенциалов, которые создают заряды каждый в отдельности. Это так называемый принцип суперпозиции.