1.14 Критерий Пирсона

Разбиваем полученные в опытах значения Tна kинтервалов:

k – число интервалов. Выдвигаем гипотезу Hо том, что выбранная теоретическая плотность вероятной случайной величины T есть функцияf(t).

В качестве величины выбираем величину , определяемую по формуле

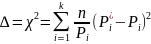
гдеn – число опытов (число отказов);

– частота попадания случайной величины Tв интервал ;

– количество значений случайной величины T, попавших в интервал ;

– вероятность попадания случайной величины T в интервал ;

; ; ;

– это случайная величина

Можно доказать, что если верна гипотеза H, то при распределение величины независимо от вида функции f(t) стремится к распределению с числом степеней свободы.

; где K– число интервалов, r–число параметров функции f(t), оцениваемых по результатам опытов, по результатам статистической выборки объёма n.

Т.е. при

Пусть –такое число, что можно считать практически невозможным осуществление событий с такой вероятностью .

Если то

Т.е, в этом случае гипотеза Hотклоняется, т.е. выбранная теоретическая плотность вероятности не согласуется с результатом опытов.

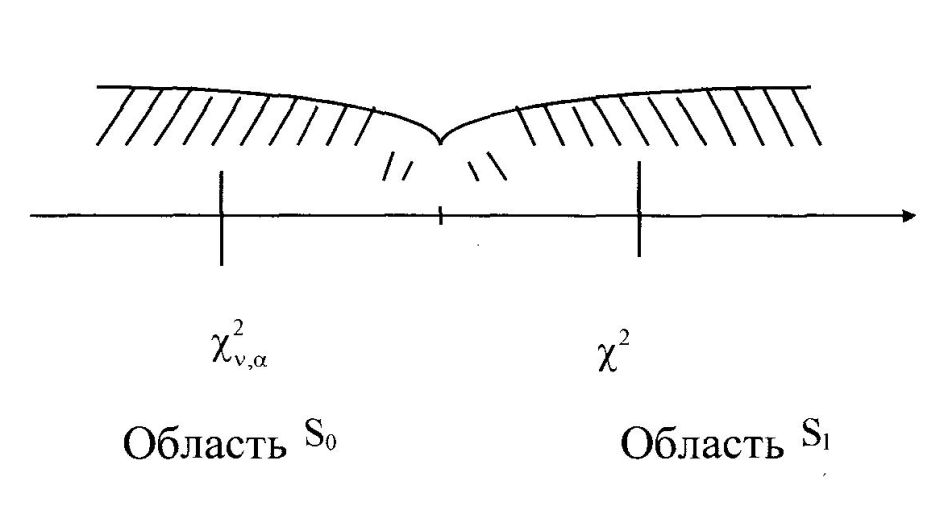
S₀ – область принятия гипотезы H(выбранная теоретическая плотность вероятности согласуется с результатами опытов)

S₁ – область отклонения гипотезы H

n_i>5, n– порядок сотен.

1.15 Критерий Колгомотова

Критерий Павлова можно применять как для непрерывных, так и для дискретных случайных величин. Критерий Колмогорова применяется только для непрерывных случайных величин.

При использовании критерия Колмогорова сравниваются статистическая функция распределения q^*(t) случайной величины Tи выбранная теоретическая функция распределения q(t). Предполагается, что значения параметров функции q(t) известны.

Если параметры теоретической функции распределения q(t) неизвестны, то вместо параметров могут использоваться оценки этих параметров, полученные по результатам опытов, т.е. по статистической выборке. В этом случае принимают .

Определяем

Определяем величину

;

- случайная величина.

Выдвигаем гипотезу Hо том, что выбранная нами теоретическая функция распределения q(t) не противоречит статистической функции распределения .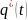

Колмогоров доказал следующую теорему.

Если верна гипотеза H, то при независимо от вида функции q(t) случайная величина имеет функцию распределения вида

тогда

Методика проверки гипотезы Hпо критерию Колмогорова;

1. Определяем статистическую функцию распределения q*(t);

2. определяем ;

3. Для заданного определяем по таблице распределения Колмогорова.

Если 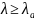, то проверяема гипотеза H отклоняется, т.е. выбранная теоретическая функция распределения q(t) не согласуется (противоречит) статистической функции распределения q*(t).

Если , то проверяема гипотеза Hпринимается, т.е. теоретическая функция распределения q(t) не противоречит функции распределения q*(t).

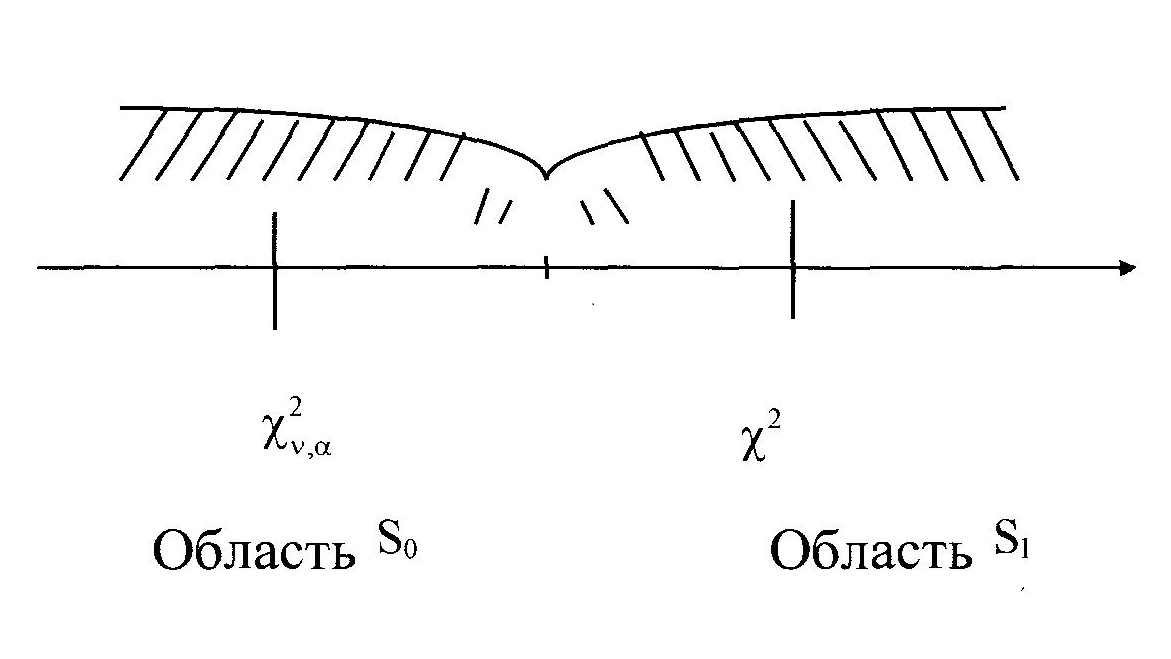
S₀ – область принятия гипотезы H,

S₁ – область отклонения гипотезы H.

1.16 Законы распределения отказов и их основные характеристики

Рассмотрим законы распределения случайной величины T, где T–время безотказной работы изделия до первого отказа (время наработки на отказ).