
- •1.Предмет оптики и эволюция представлений о природе света.
- •2. Геометрическая оптика. Законы геометрической оптики.
- •3. Центрированная оптическая система.
- •4. Формулы оптической системы
- •5. Тонкие линзы
- •6. Лупа. Зрительная труба. Микроскоп.
- •7. Глаз и зрение
- •8. Интерференция световых волн
- •10. Классические интерференционные опыты
- •11 Интерферометры
- •12 Многолучевая интерференция: а)интерференция лучей одинаковой интенсивности; б)интерференция лучей с монотонно убывающей интенсивностью.
- •13 Практические применения интерференции
- •14 Дифракция света виды дифракции
- •Дифракция от круглого отверстия
- •Корню спираль
- •Дифракция света на одной щели
- •Дифракция света на дифракционной решетке
- •17 Основные фотометрические и светотехнические величины
- •18 Тепловое излучение. Закон Кирхгофа
- •20 Оптическая пирометрия. Оптические методы измерения температуры.
- •21 Поляризация света. Линейно-поляризованный свет.
- •22. Получение поляризованного света. Двойное лучепреломление в кристаллах. Призма Николь.
- •23 Вращение плоскости поляризации. Поляризация света при отражении
- •24. Дисперсия света. Электронная теория дисперсии света.
- •25 Ослабление оптического излучения в мутных средах.
- •26. Фотоэффект. Внешний и внутренний фотоэффект. Фотогальванический эффект.
- •27. Эффект Комптона. Элементарная теория эффекта Комптона.
- •28. Давление света. Опыты Лебедева.
- •29. Фотохимическое действие света. Законы фотохимии. Сенсибилизаторы.
- •30.Физические основы фотографии. Цветная фотография: субтрактивный метод и метод Липпмана.
- •31.Голография. Физические основы голографии и трудности ее технической реализации.
- •32.Опыты Резерфорда. Планетарная модель атома.
- •33.Постулаты Бора. Теория Бора для водородного атома. Недостатки теории Бора.
- •34.Гипотеза Де-Бройля. Корпускулярно-волновой дуализм.
- •35.Волновая функция. Уравнение Шредингера.
- •36.Спонтанное и вынужденное излучение света атомами. Лазеры.
- •37.Атомное ядро. Ядерные реакции.
- •38.Закон радиоактивного распада. Цепная реакция деления ядер.
Дифракция от круглого отверстия
Поставим
на пути сферической световой волны
непрозрачный экран с круглым отверстием
радиуса ![]() .
Экран расположен так, что перпендикуляр,
опущенный из S на
непрозрачный экран, попадает точно в
центр отверстия (рис. 9.3).
.
Экран расположен так, что перпендикуляр,
опущенный из S на
непрозрачный экран, попадает точно в
центр отверстия (рис. 9.3).
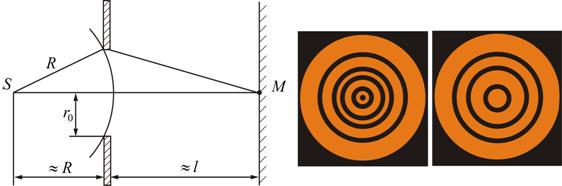
Рис. 9.3
На продолжении этого перпендикуляра возьмем точку M и рассмотрим, что мы будем наблюдать на экране.
Разобьем открытую часть волновой поверхности на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке М всеми зонами (9.2.1) и (9.2.2),
|
|
(9.3.1) |
|
Таким образом, когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке М будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю, как показано на рис. 9.3.
Естественно,
что если ![]() ,
то никакой дифракционной картины не
будет.
,
то никакой дифракционной картины не
будет.
Корню спираль
КОРНЮ
СПИРАЛЬ (по
имени М. А. Корню, М. А. Соrnu) (клотоида) -
кривая, используемая для графич.
вычисления распределения интенсивности
при дифракции
светана
прямолинейном крае или на щели
(дифракция Фраунгофера);
состоит из двух симметричных ветвей,
бесконечное число раз обвивающихся
вокруг "фокусов" F и ![]() и
неограниченно приближающихся к ним.
и
неограниченно приближающихся к ним.
Ур-ние К. с. в параметрич. форме имеет вид Френеля интегралов:
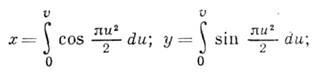
"фокусы" ![]() и
и ![]() -
асимптотич. точки кривой; пределы
интегрирования определяются размерами
щелей и экранов, на к-рых происходит
дифракция.
-
асимптотич. точки кривой; пределы
интегрирования определяются размерами
щелей и экранов, на к-рых происходит
дифракция.
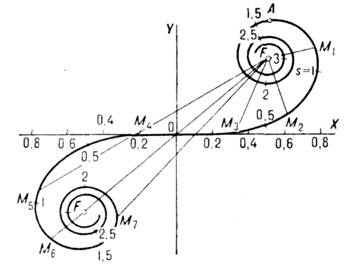
Относит.
амплитуда волны при
дифракции на крае экрана зависит от
длины вектора, проведённого из точки F в
разл. точки К. с. (напр.,М1![]() М7).
Скольжение вектора по правой (верх.)
ветви спирали (FMl, FH2, FM3)определяет
плавно уменьшающуюся амплитуду волны
в области геом. тени; амплитуда на границе
тени соответствует вектору FO; скольжение
вектора по левой (ниж.) части спирали
(FM4, FM5, FM6,FM7,)даёт
дифракц. полосы в освещённой области.
Амплитуда волны в отсутствие экрана
или вдали от границы геом. тени определяется
вектором
М7).
Скольжение вектора по правой (верх.)
ветви спирали (FMl, FH2, FM3)определяет
плавно уменьшающуюся амплитуду волны
в области геом. тени; амплитуда на границе
тени соответствует вектору FO; скольжение
вектора по левой (ниж.) части спирали
(FM4, FM5, FM6,FM7,)даёт
дифракц. полосы в освещённой области.
Амплитуда волны в отсутствие экрана
или вдали от границы геом. тени определяется
вектором![]()
16 Дифракция Фраунгофера на щели и на системе щелей. Дифракционные решетки.
Тип дифракции, при котором дифракционная картина образуется параллельными пучками, называется дифракцией Фраунгофера. Параллельные лучи проявятся, если источник и экран находятся в бесконечности. Практически используется две линзы: в фокусе одной – источник света, а в фокусе другой – экран.
Хотя принципиально дифракция Фраунгофера не отличается от дифракции Френеля, но практически именно этот случай важен, так как именно этот тип дифракции используется во многих дифракционных приборах (дифракционная решетка, например). Кроме того, здесь математический расчет проще и позволяет решать количественную задачу до конца (дифракцию Френеля мы рассматривали качественно).
Дифракция света на одной щели
Пусть
в непрерывном экране есть щель: ширина
щели ![]() ,
длина щели (перпендикулярно плоскости
листа)
,
длина щели (перпендикулярно плоскости
листа) ![]() (рис.
9.5). На щель падают параллельные лучи
света. Для облегчения расчета считаем,
что в плоскости щели АВ амплитуды
и фазы падающих волн одинаковы.
(рис.
9.5). На щель падают параллельные лучи
света. Для облегчения расчета считаем,
что в плоскости щели АВ амплитуды
и фазы падающих волн одинаковы.
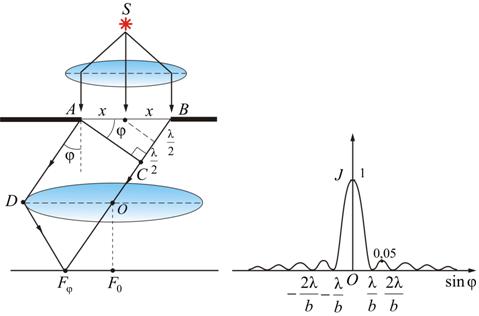
Рис. 9.5
Разобьем
щель на зоны Френеля так, чтобы оптическая
разность хода между лучами, идущими от
соседних зон, была равна ![]() .
.
Если
на ширине щели укладывается четное
число таких зон, то в точке ![]() (побочный
фокус линзы) будет
наблюдаться минимум интенсивности, а
если нечетное число зон, то максимум
интенсивности:
(побочный
фокус линзы) будет
наблюдаться минимум интенсивности, а
если нечетное число зон, то максимум
интенсивности:
|
|
(9.4.1) |
|
|
|
(9.4.2) |
|
Картина
будет симметричной относительно главного
фокуса точки ![]() .
Знак плюс и минус соответствует углам,
отсчитанным в ту или иную сторону.
.
Знак плюс и минус соответствует углам,
отсчитанным в ту или иную сторону.
Интенсивность
света ![]() .
Как видно из рис. 9.5, центральный максимум
по интенсивности превосходит все
остальные.
.
Как видно из рис. 9.5, центральный максимум
по интенсивности превосходит все
остальные.
Рассмотрим влияние ширины щели.
Т.к.
условие минимума имеет вид ![]() ,
отсюда
,
отсюда
|
|
(9.4.3) |
|
Из этой формулы видно, что с увеличением ширины щели b положения минимумов сдвигаются к центру, центральный максимум становится резче.
При уменьшении ширины щели b вся картина расширяется, расплывается, центральная полоска тоже расширяется, захватывая все большую часть экрана, а интенсивность ее уменьшается.

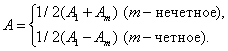
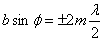 – условие
минимума интенсивности;
– условие
минимума интенсивности;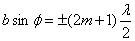 – условие
максимума интенсивности
– условие
максимума интенсивности