
- •Московский авиационный институт
- •1. Объект характеризуется четырьмя равноценными критериями: f1, f2, f3, f4.
- •3. Как графически выглядит множество Парето для пары критериев f1, f3 из предыдущей задачи ?
- •4. Вы можете положить деньги в один из трех банков a, b, c. Месячный дивиденд зависит от непредсказуемой налоговой политики правительства и определяется таблицей:
- •7. Три места работы a, b и с характеризуются месячной зарплатой, продолжительностью отпуска и климатом в отношениях между людьми в соответствии со следующей таблицей
- •8. Объект выбора характеризуется тремя критериями f1, f2, f3, где:
Московский авиационный институт
( Национально Исследовательский университет)
Факультет: РАДИОВТУЗ МАИ.
Курсовая работа по дисциплине.
«Основы теории принятия инженерных решений».
Вариант № 7.
Выполнил: студент 2-го курса
группы РО-203Б
Корнеев Александр.
Проверил преподаватель:
Ильин В.Н.
Москва 2014.
Задание курсовой работы (Задание 7).
1. Объект характеризуется четырьмя равноценными критериями: f1, f2, f3, f4.
где : F1, F3 - критерии, характеризующие положительные свойства объекта;
F2, F4 - критерии, характеризующие отрицательные свойства объекта.
Таблица принятия решений для выбора наилучшего из трех объектов A, B, C имеет следующий вид:
-
Тип
объекта
Критерии
F1
F2
F3
F4
А
20
14
18
10
В
12
24
26
15
С
20
17
42
25
Определите наилучший объект, применяя:
а) аддитивный критерий
б) мультипликативный критерий
в) критерий минимального удаления от идеала.
Определим наилучший объект, применяя сначала аддитивный критерий. Произведём нормализацию по формуле:
![]()
Получим следующие значения, с которыми будем деле работать:
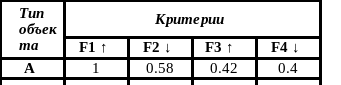
Воспользуемся аддитивным критерием:
![]()
причём,
по условию задачи, критерии равноценны
(весовых коэффициентов нет), следовательно,
![]() ,
а значит, его можно не учитывать в
расчётах.
,
а значит, его можно не учитывать в
расчётах.
Получаем:
Y(a)=1-0.58+0.42-0.4=0,44
Y(b)=0.6-1+0,6 -0,6=-0,4
Y(c)=1-0.7+1-1=0,3
Отсюда следует, что в данном случае лучшая альтернатива – A.
Применим мультипликативный критерий:
![]() ;
;
так
как критерии равноценны, то
![]()
Y(a)=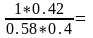 0,76
0,76
Y(b)=
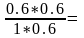 0,6
0,6
Y(c)=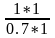 =1,4
=1,4
Из расчёта по мультипликативному критерию следует, что лучшей альтернативой является С.
Используем метод минимального удаления от идеала.
Формула для метода выглядит следующим образом:
![]()
Идеалы
для каждого критерия:
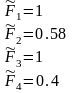
Y(a)=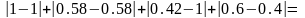
Y(b)=
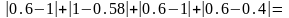
Y(c)=
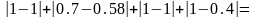
Из результатов видно, что лучшей альтернативой оказывается C.
2 . В задаче 1 задайтесь конкретным типом объекта (компьютер, автомобиль и т.д.) и укажите названия его критериев F1, F2, F3, F4 (производительность, скорость, цена и т.д. ) с учётом их положительного или отрицательного смысла, указанного в условиях задачи 1.
Определите приоритеты критериев, расставьте критерии по приоритету и вычислите весовые коэффициенты.
Снова определите наилучший объект по тем же трём обобщённым критериям , что и в предыдущей задаче и сравните результаты.
Зададим в качестве типа объекта планшетный компьютер.
Тогда критерии будут иметь следующий смысл:
F1-производительность
F2-вес
F3-память
F4-цена
Проранжируем критерии:
-
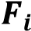
F1
F2
F3
F4
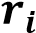
1
3
2
4
Переход от рангов к оценкам производится по следующей формуле:
![]()
где n – число критериев.
![]()
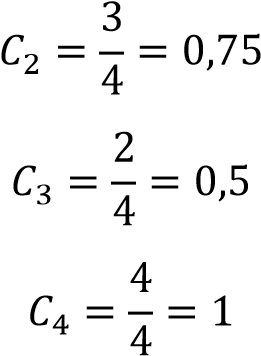
Применим аддитивный метод:
Y(a)=0.25*1-0.75*0.58+0.5*0.42-1*0.4=0,44
Y(a)=1*0.25-0.82*0.75+0.67*0.5-0.71*1=0.74
Y(b)=0.6*0.25-1*0.75+0.83*0.5-1*1=1.19
Y(c)=0.7*0.25-0.78*0.75+1*0.5-0.6*1=-0.55
В данном случае предпочтительней вариант B.
Теперь применим мультипликативный метод:
Y(a)=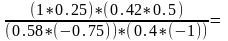 0,76
0,76
Y(a)=1^(0.25)*0.22^(-0.75)*0.67^(0.5)*0.71(-1)=3.6
Y(b)=0.6^(0.25)*1^(-0.75)*0.83^(0.5)*1^(-1)=0.8
Y(c)=0.7^(0.25)*0.78^(-0.75)*1^(0.5)*0.86^(-1)=1.75
Лучшей альтернативой является А.
Используем метод минимального удаления от идеала:
Y(a)=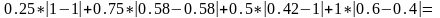
Y(a)=
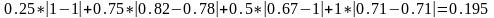
Y(b)=

Y(c)=
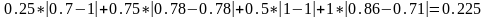
Лучшей альтернативой является А.
