88. Понятие и формула коэффициента детерминации.

89. Выборочные уравнения линейной регрессии через коэффициент регрессии, через коэффициент корреляции.

Корреляционную зависимость от можно описать с помощью уравнения вида

(1)

г де условное среднее величины , соответствующее значению величины , а некоторая функция. Уравнение (1) называется выборочным уравнением регрессии на .

Рис.1. Линейная регрессия значима. Модель .

Функцию называют выборочной регрессией на , а ее график – выборочной линией регрессии на .

Совершенно аналогично выборочным уравнением регрессии на является уравнение .

Линейная регрессия

Выбрав вид функции регрессии, т.е. вид рассматриваемой модели зависимости от Х (или Х от У), например, линейную модель , необходимо определить конкретные значения коэффициентов модели.

При различных значениях а и можно построить бесконечное число зависимостей вида т.е на координатной плоскости имеется бесконечное количество прямых, нам же необходима такая зависимость, которая соответствует наблюдаемым значениям наилучшим образом. Таким образом, задача сводится к подбору наилучших коэффициентов.

90. Задачи регрессионного анализа.

91. Задачи корреляционного анализа.

92. Коэффициент линейной корреляции Пирсона, его свойства.

• колебаний оКоэффициент корреляции, который одним числом дает представление о направлении и силе связи между признаками (явлениями);

пределы его т 0 до +1

• М 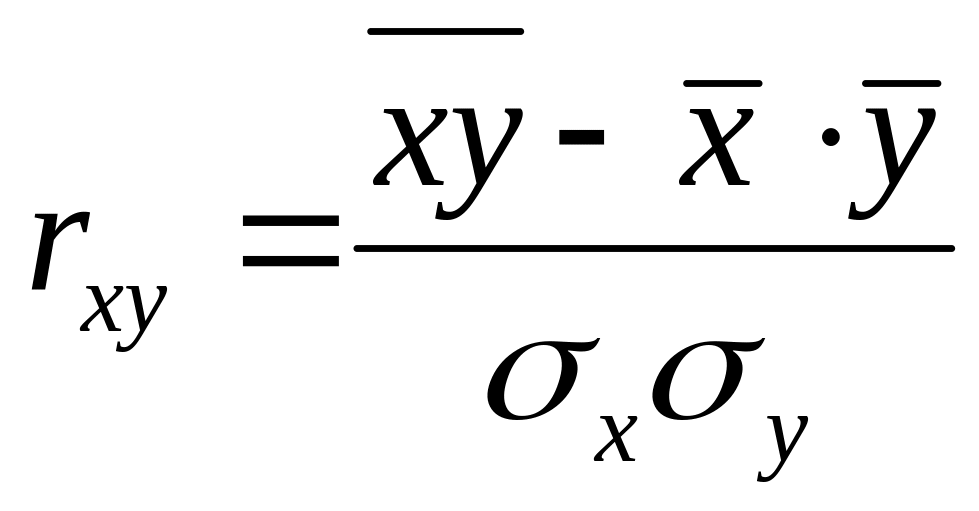етод квадратов (метод Пирсона)

Рекомендации к применению метода квадратов (Пирсона)

• Когда требуется точное установление силы связи между признаками;

• Когда признаки имеют только количественное выражение.

93. Сила и характер корреляционной связи, соответствие им коэффициента корреляции.

Сила и характер связи между параметрами

Сила связи	Характер связи
	Прямая (+)	Обратная (-)
Полная	1	-1
Сильная	От 0,7 до 1	От -0,7 до -1
Средняя	От 0,699 до 0,3	От -0,699 до -0,3
Слабая	От 0,299 до 0	От -0,299 до 0
Связь отсутствует	0	0

94. t – статистика критерия значимости коэффициента корреляции.

Проверка гипотезы о значимости коэффициента корреляции.

О статистической взаимосвязи говорят, что она существует или отсутствует, имеет направление и характеризуется силой.

Если в результате исследования нулевая гипотеза не отвергается, то «взаимосвязи нет» . В случае, когда нулевая гипотеза отклоняется говорят о существовании связи исследуемых случайных величин.

1. Сформулируем гипотезы H₀ и H₁:

H₀: r =0 (корреляции нет),

H₁: r ≠0.

2. З 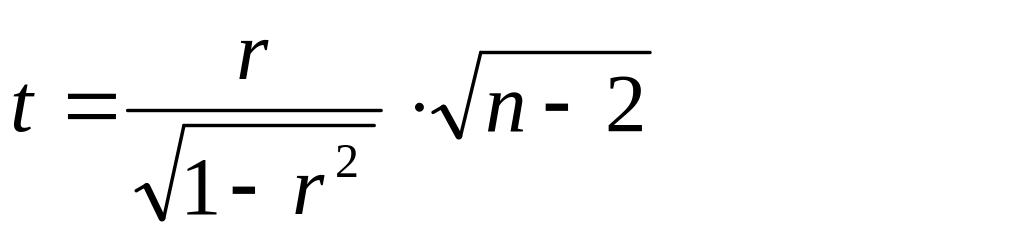ададим уровень значимости α.

3. Статистика критерия

4. t_{α,n-2 .} t-статистика, имеющая распределение Стьюдента с (n-2) степенями свободы.

2. При │t│≥ t_α,n-2 , H₀ отвергается. Это значит, что между параметрами существует значимая корреляция. При │t│< t_α,n-2 , H₀ принимается.

Достоверность определяется по формуле:

Критерий t оценивается по таблице значений t с учетом числа степеней свободы (n-2), где n – число парных вариант.

Критерий t должен быть равен или больше табличного, соответствующего вероятности p ≥ 95 %

95. Коэффициент ранговой корреляции Спирмена.

• Ранговый метод (метод Спирмена)

Рекомендации по применению метода ранговой корреляции (Спирмена)

• Когда нет необходимости в точном установлении силы связи, а достаточно ориентировочных данных;

• Когда признаки не только количественные, но и атрибутивные;

• Когда ряды распределения признаков имеют открытые варианты

(например, стаж работы до 1 года).

\

96. Последовательность операций при применении статистических методов для обработки данных.

• четкое формулирование задачи в терминах специальной науки,

• перевод задачи на язык статистики,

• выбор пригодного метода для ее решения,

• проведение необходимых вычислений,

• исходя из полученных результатов, формулирование выводов в терминах статистической науки,

• формулирование вывода на языке специальной науки.

97. Этапы медико-биологического эксперимента.

• планирование,

• проведение эксперимента,

• статистический анализ полученных данных

• описание результатов;

• выводы.

98. Что включает в себя планирование медико-биологического эксперимента.

• определение цели исследования,

• описание популяции,

• определение выборки,

• формулирование гипотезы,

• определение уровня значимости,

• определение мощности критерия.

99. Что включает в себя проведение медико-биологического эксперимента.

• производство выборок в соответствии с планом,

• создание файла или таблицы с результатами измерений.

100. Что включает в себя анализ медико-биологического эксперимента.

• проверка корректности собранных данных,

• статистический анализ.

101. Что включает в себя статистический анализ медико-биологического эксперимента.

• визуализацию данных (графическое представление данных – построение полигонов, гистограмм),

• проверку гипотез о виде выборочного распределения,

• оценку параметров распределения (точечное и интервальное оценивание),

• выявление связей и зависимостей.

102. Что подразумевают под выводами при проведении анализа данных медико-биологического эксперимента.

• подробно описываются результаты эксперимента и статистического анализа.

103. Виды планов клинических исследований и их границы применимости.

• параллельный,

• перекрестный,

• факторный,

• последовательный.