Основные вопросы темы:

1. Понятие статистики – как науки.

Статистика. - Это наука, позволяющая увидеть закономерности в хаосе случайных данных, выделить устойчивые связи в них, определить действия с тем, чтобы увеличить долю правильно принятых решений среди всех принимаемых. Это сбор, группировка, систематизация, представление, анализ и интерпретация данных (результатов наблюдений). Это изучение генеральных совокупностей и их изменчивости.

2. Понятие биологической статистики.

Биологическая статистика - система знаний о правилах планирования и анализа результатов натурных и экспериментальных исследований биологических объектов.

3. Предмет, цель и задачи биологической статистики

Предмет – основные положения и методы биологической статистики.Цель дисциплины – научить правильно количественно оценивать процессы, происходящие в живой природе.Задачи дисциплины – познакомить и научить пользоваться основными статистическими критериями для оценки биологических совокупностей

4. Понятие термина «переменная».

Переменные просто определяют категории, каждая из которых описывает некоторое качество, присущее переменной; таким образом можно классифицировать объект, человека или свойство.Категориям может быть присвоено нечисловое обозначение (например, раса, пол) или числовой код (например, идентификационный номер пациента).

5. Типы данных.

6. Типы и характеристики качественных данных.

Номинальные или категориальные (классификационные):

Данные разбиты на категории, названия которых отражают значения признака или классификационный номер.

Данные этого типа нельзя измерять или упорядочивать по значению, над ними нельзя выполнять арифметические операции.

Примеры: пол, семейное положение, этническая группа, статус занятости, группа крови.

Порядковые (ранговые):

Данные относятся к непересекающимся категориям, в зависимости от степени проявления у них анализируемого признака. Категории (градации, уровни) логически упорядочены в соответствии со шкалой относительной значимости значений.

Над данными нельзя выполнять арифметические операции.

Примеры: стадии заболевания, выраженность боли (шкала оценки боли), классы общества.

Бинарные или дихотомические:

Номинальные или категориальные данные, которые распределяются по двум непересекающимся категориям.

Примеры: мертвый / живой, излеченный / не излеченный.

7. Типы и характеристики количественных данных.

Непрерывные числовые :

Данные могут принимать любое числовое значение из заданного диапазона (отрезка). Количество значений бесконечно, значения могут содержать дробную составляющую, зависящую от точности измерений.

Примеры: температура, вес, рост, давление.

8. Основные типы измерительных шкал и их характеристики.

Шкала – необходимый, обязательный элемент измерительной процедуры.

Основные типы измерительных шкал:

• Номинальная или категориальная,

Переменные просто определяют категории, каждая из которых описывает некоторое качество, присущее переменной; таким образом можно классифицировать объект, человека или свойство.

Категориям может быть присвоено нечисловое обозначение (например, раса, пол) или числовой код (например, идентификационный номер пациента).

• Порядковая или оценочная,

Величины могут быть упорядочены по значению, в зависимости от степени выраженности присущего им признака (например, размера, ценности, сложности) без точного определения расстояния (разности) между категориями.

• Интервальная.

Интервалы между наблюдениями выражаются в фиксированных единицах измерения.

Интервальная шкала показывает размах отдельных измерений признака.

Пример: некоторые шкалы температуры (Фаренгейта, Цельсия)

Некоторые интервальные шкалы являются циклическими (времена года, время суток).

9. Необходимость использования графических методов представления данных.

Применяется для:

• Распознавания структуры и характерных особенностей

данных;

• Обнаружения ошибок в данных;

• Исследования взаимосвязи между случайными

величинами;

• Оценки соответствия данных выбранным моделям;

• Обнаружения новых явлений;

• Выявления необходимости в корректировке данных, а

также определения способа ее осуществления

(преобразование данных, сбор дополнительных данных

или изменение условий эксперимента).

10. Основные графики, представляющие дискретные данные.

• Таблица

• Столбиковая диаграмма

• Круговая диаграмма

• Точечный график

• и т.д.

11. Основные графики, представляющие непрерывные данные.

• Группированная выборка

• Гистограмма

• Полигон частот

• Диаграмма «Стебель с листьями»

• и т.д.

12. Определение статистической совокупности.

Множество объектов, характеризуемых некоторым качественным или количественным признаком, называется статистической совокупностью.

13. Определение генеральной статистической совокупности.

Статистическая совокупность, состоящая из всех объектов, которые ( по крайней мере, теоретически) подлежат обследованию, называется генеральной статистической совокупностью

14. Понятие выборочного метода.

Метод статистического исследования, состоящий в том, что на основе изучения выборочной совокупности делается заключение о всей генеральной совокупности, называется выборочным методом.

15. Определение выборочной совокупности или выборки.

Статистическая совокупность, состоящая из некоторого количества объектов, случайным образом отобранных из соответствующей генеральной совокупности, называется выборочной совокупностью или просто выборкой.

16. Основные требования к выборочной совокупности. Понятие репрезентативности.

Основные требования к выборке – хорошо представлять генеральную совокупность, то есть быть представительной (репрезентативной).

Репрезентативность:

• случайностью выбора объектов из генеральной совокупности, когда каждому из них обеспечивается одинаковая возможность быть отобранным;

• независимостью результатов наблюдений в выборе;

• правильным определением объема выборки с учетом всех конкретных условий.

17. Основные виды способов отбора данных.

Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.

Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.

На практике обычно пользуются бесповторным случайным отбором.

На практике применяются различные способы отбора. Принудительно эти способы можно подразделить на два вида:

. Отбор, не требующий расчленения генеральной совокупности на части, сюда относятся:

а) простой случайный бесповторный отбор;

б) простой случайный повторный отбор.

. Отбор, при котором генеральная совокупность разбивается на части, сюда относятся:

а) типический отбор;

б) механический отбор;

в) серийный отбор.

Простым случайным называют такой отбор, при котором объекты извлекают по одному из всей генеральной совокупности. Если извлеченные карточки не возвращать в пачку, то выборка будет простой случайной бесповторной.

Типическим называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типической» части.

Механическим называют отбор, при котором генеральная совокупность «механически» делится на столько групп, сколько объектов должно войти в выборку, и из каждой группы отбирается один объект.

Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергаются сплошному обследованию.

18. Понятия объема совокупности, варианты, частоты и относительной частоты, их обозначения.

Число элементов генеральной совокупности называется ее объемом.

Часть генеральной совокупности, случайным образом отобранная для наблюдений, называется случайной выборкой или, для краткости, выборкой.

Число элементов выборки называется ее объемом.

Число наблюдений варианты называют частотой, а ее отношение к объему выборки - относительной частотой .

19. Определение вариационного ряда.

Пусть из генеральной совокупности извлечена выборка, причем х₁ наблюдалось п₁ раз, х₂ – п₂ раз, х_к – п_к раз и - объем выборки. Наблюдаемые значения х₁ называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом.

20. Определения дискретного и интервального статистических распределений.

Статистическим (эмпирическим) законом распределения выборки, или просто статистическим распределением выборки называют последовательность вариант и сответствующих им частот п_i или относительных частот .

Статистическое распределение выборки удобно представлять в форме таблицы распределения частот, называемой статистическим дискретным рядом распределения:

`

х1	х2	…
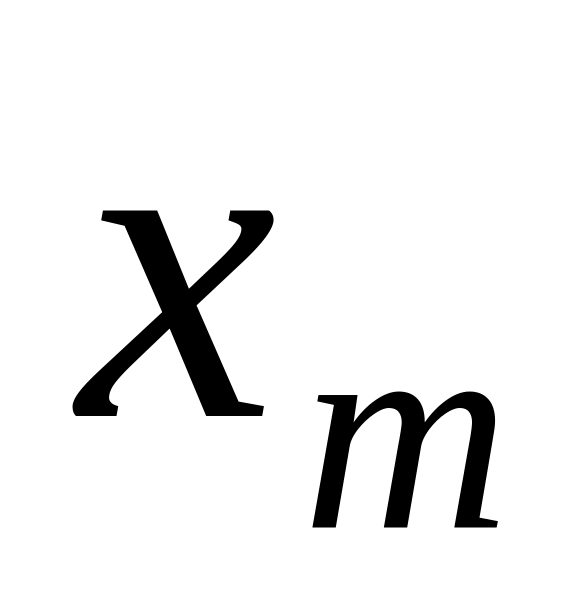
п1	п2	…

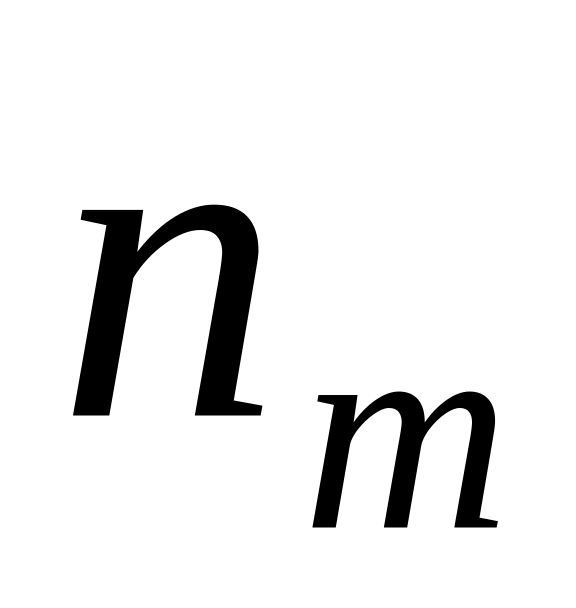
(сумма всех частот равна объему выборки )

или в виде таблицы распределения относительных частот:

х1	х2	…
w1	w2	…

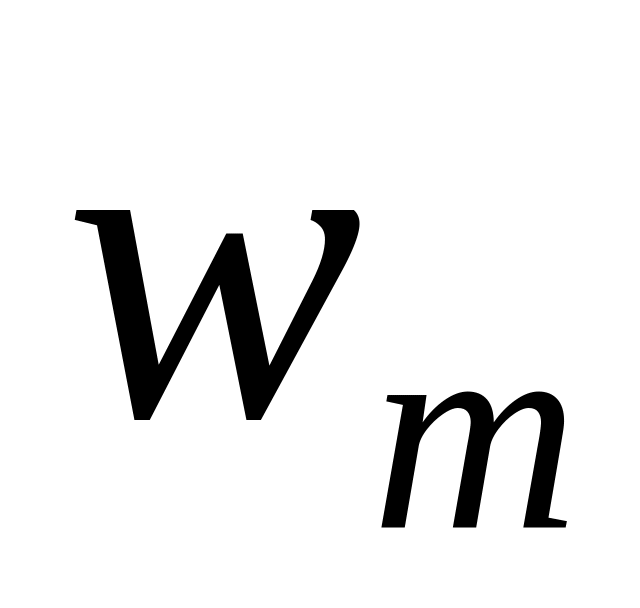
(сумма всех относительных частот равна единице ).

Пример 1. При измерениях в однородных группах обследуемых получены следующие выборки: 71, 72, 74, 70, 70, 72, 71, 74, 71, 72, 71, 73, 72, 72, 72, 74, 72, 73, 72,74 (частота пульса). Составить по этим результатам статистический ряд распределения частот и относительных частот.

Решение. 1) Статистический ряд распределения частот:

хi	70	71	72	73	74
пi	2	4	8	2	4

2) Объем выборки: п=2+4+8+2+4=20. Найдем относительные частоты, для чего разделим частоты на объем выборки :

;

Напишем распределение относительных частот:

хi	70	71	72	73	74
wi	0,1	0,2	0,4	0,1	0,2

Контроль: 0,1+0,2+0,4+0,1+0,2=1.

Полигоном частот называют ломаную, отрезки, которой соединяют точки Для построения полигона частот на оси абсцисс откладывают варианты х₂, а на оси ординат – соответствующие им частоты п_i. Точки соединяют отрезками и получают полигон частот.

Полигоном относительных частот называют ломаную, отрезки, которой соединяют точки . Для построения полигона относительных частот на оси абсцисс откладывают варианты х_i, а на оси ординат соответствующие им частоты w_i. Точки соединяют отрезками и получают полигон относительных частот

Пример 2. Постройте полигон частот и полигон относительных частот по данным примера 1.

Решение: Используя дискретный статистический ряд распределения, составленный в примере 1 построим полигон частот и полигон относительных частот:

2 . Статистический интервальный ряд распределения. Гистограмма. Статистическим дискретным рядом (или эмпирической функцией распределения) обычно пользуются в том случае, когда отличных друг от друга вариант в выборке не слишком много, или тогда, когда дискретность по тем или иным причинам существенна для исследователя. Если же интересующий нас признак генеральной совокупности Х распределен непрерывно или его дискретность нецелесообразно ( или невозможно) учитывать, то варианты группируются в интервалы.

Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).

1. R(размах) =X_max –X_min

2. k-число групп

3. (формула Стерджеса)

4. a=x_min, b=x_max

5.

Полученную группировку удобно представить в форме частотной таблицы, которая носит название статистический интервальный ряд распределения:

Интервалы группировки			...
Частоты			...

_{Аналогическую таблицу можно образовать, заменяя частоты ni относительными частотами :}

Интервалы группировки			...
Отн. частоты			...

21. Понятия полигона и гистограммы частот и относительных частот.

Полигоном частот называют ломаную, отрезки, которой соединяют точки Для построения полигона частот на оси абсцисс откладывают варианты х₂, а на оси ординат – соответствующие им частоты п_i. Точки соединяют отрезками и получают полигон частот.

Полигоном относительных частот называют ломаную, отрезки, которой соединяют точки . Для построения полигона относительных частот на оси абсцисс откладывают варианты х_i, а на оси ординат соответствующие им частоты w_i. Точки соединяют отрезками и получают полигон относительных частот

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению (плотность частоты).

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии . Площадь i-го частичного прямоугольника равна - сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

Г истограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению (плотность относительной частоты).

22. Чему равны площади частичных прямоугольников и суммы площадей частичных прямоугольников гистограммы частот и относительных частот.

Площадь i-го частичного прямоугольника равна - относительной частоте вариант, попавших в i-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.

23. Чему соответствует максимальная точка полигона частот.

24. Определение, обозначение и формула расчета выборочной средней.

Выборочной средней называют среднее арифметическое значение признака выборочной совокупности:

, или .

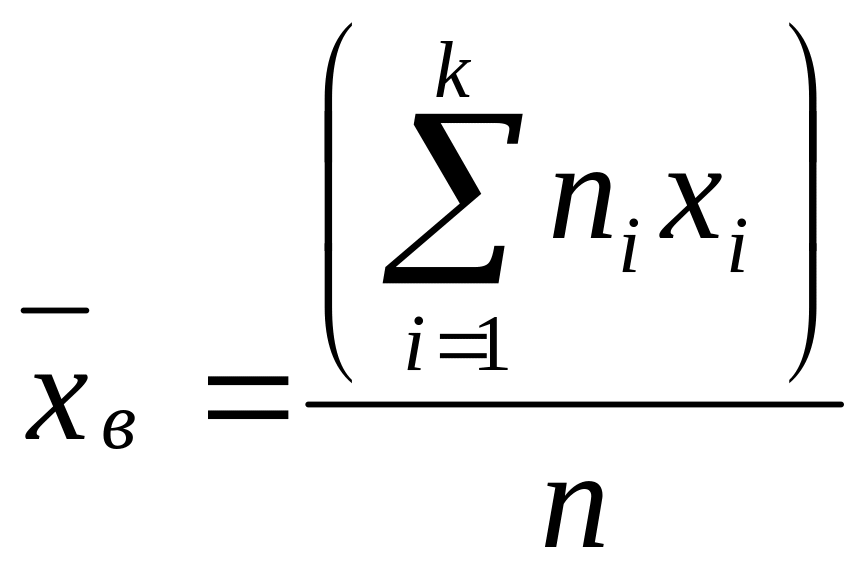х_i – варианта выборки, п_i – частота варианты х_i, - объем выборки.

25. Определение, обозначение и формула расчета выборочного среднего квадратического отклонения.

Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выброчной дисперсии:

.

26. Числовые характеристики вариационного ряда мода и медиана, их обозначения и способы нахождения.

Пусть из генеральной совокупности извлечена выборка, причем х₁ наблюдалось п₁ раз, х₂ – п₂ раз, х_к – п_к раз и - объем выборки. Наблюдаемые значения х₁ называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом.

Число наблюдений варианты называют частотой, а ее отношение к объему выборки - относительной частотой .

Выборочная медиана – это середина вариационного ряда, значение, расположенное на одинаковом расстоянии от левой и правой границы выборки.

Выборочная мода – это наиболее вероятное, т.е. чаще всего встречающееся, значение в выборке.

27. Понятие и формула вычисления выборочной дисперсии.

Смещенной оценкой генеральной дисперсии служит выборочная дисперсия:

.

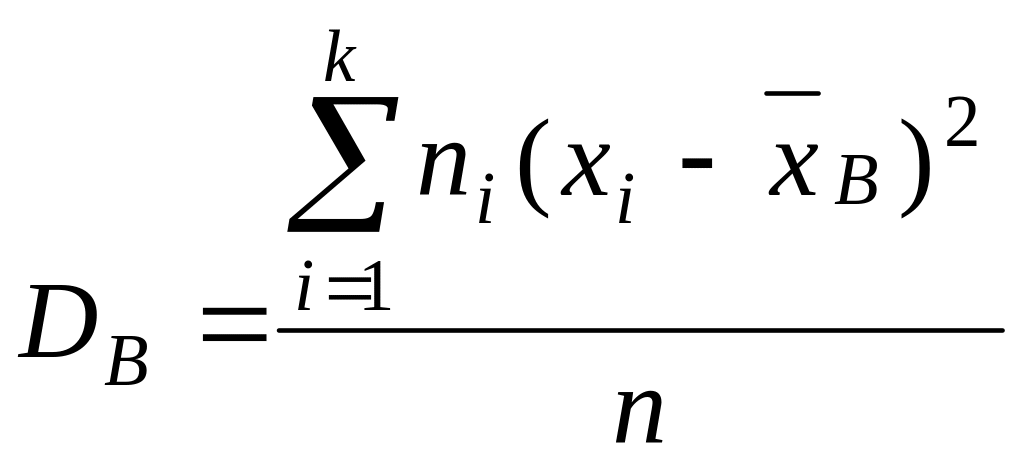Более удобна формула:

28. Виды ошибок выборочного обследования.

Величину отклонения выборочного показателя (статистики) от его генерального пара­метра называют статистической ошибкой. Для измерения этой ошибки некоторой статистики квадратичная (стандартная) ошибка статистики (нельзя путать со средним квадратичным от­клонением изучаемой случайной переменной):

Величину отклонения выборочного показателя (статистики) от его генерального пара­метра называют статистической ошибкой. Для измерения этой ошибки некоторой статистики квадратичная (стандартная) ошибка статистики (нельзя путать со средним квадратичным от­клонением изучаемой случайной переменной). Так, стандартная ошибка среднего арифметиче­ского может быть найдена по формуле:

Д

29. Нормальное распределение; график; параметры, описывающие нормальное распределение.Нормальное распределение впервые было найдено Абрахамом де Муавром в первой половине XVIII в. (1733г). Затем в начале XIX в. было использовано в работах Гаусса и Лапласа и, по существу, было открыто заново. Под влиянием классических работ Гаусса и Лапласа долгие годы считалось непререкаемой истиной, что все возможные распределения при достаточно большом количестве наблюдений приближаются к нормальному распределению, как некоему идеалу. Подобное утверждение, безусловно, слишком смелое, но тем не менее множество биологических и медицинских показателей, таких как показатели физического развития (вес, рост, давление, температура тела, уровень гормонов), составляющие плазмы крови, демографические и другие показатели следуют нормальному распределению. Нормальное распределение представляет собой семейство кривых. Каждая кривая это колоколообразный график, на котором по горизонтальной оси откладывается величина эффекта, а на вертикальной – количество пациентов, у которых наблюдался эффект данной величины.

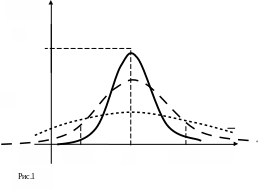Кривая полностью определяется двумя параметрами, средним и среднеквадратическим отклонением. Факт указанного распределения записывают таким образом: .

30. Основные характеристики нормального распределения.

равенство числовых характеристик

- симметричность отклонений от среднего значения;

- общая площадь под кривой равна 1;

- хвосты кривой асимптотически стремятся к горизонтальной оси;

- форма кривой определяется среднеквадратическим отклонением генеральной совокупности;

- 68,25% всех значений лежит в интервале ±σ (±1 среднеквадратическое отклонение от среднего);

95,44% всех значений лежит в интервале ±2σ (±2 среднеквадратических отклонений от среднего);- 99,73% всех значений лежит в интервале ±3σ (±3 среднеквадратических отклонений от среднего).

31.Понятия точечной и интервальной оценок параметров распределения.

Точечной называют оценку, которая определяется одним числом.

Интервальная - двумя числами.

32.Оценки Точечные оценки параметров ген. совокупности:параметров генеральной совокупности.

г енеральная средняя:

 Интервальные оценки параметров совокупности.

Интервал, который с заданной вероятностью (надежностью) покрывает неизвестный параметр, называется доверительным интервалом.

Вероятности, признанные достаточными для уверенного суждения о генеральных параметрах на основании известных выборочных показателей, называются доверительными вероятностями.

31. Доверительный интервал.

Интервал, который с заданной вероятностью (надежностью) покрывает неизвестный параметр, называется доверительным интервалом.

Д оверительный интервал для выборочного среднего значения:

32. Формулы для нахождения количества интервалов, шага интервала, размаха.

1. R(размах) =X_max –X_min

2. k-число групп

3. (формула Стерджеса)

4. a=x_min, b=x_max

5.