Метод Рунге-Кутта четвертого порядка точности
yi=
,
где
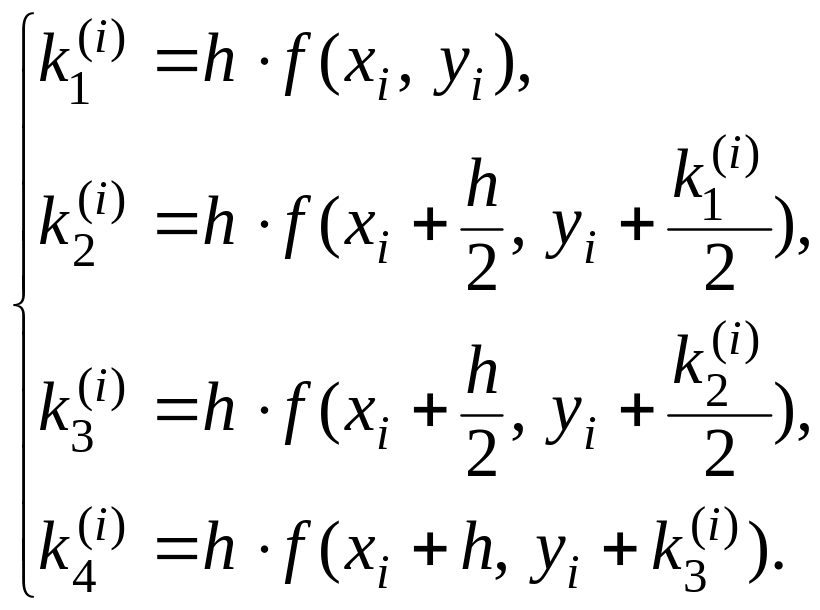
Абсолютная погрешность находится с помощью равенства
|
-y(xi)|
|
-
yi|,
i=1,2,…,n.
Контрольные вопросы
Каковы условия существования и единственности решения задачи Коши?
К какой группе методов относится метод последовательных приближений решения задачи Коши?
Как формулируется задача численного интегрирования дифференциального уравнения?
Какой способ оценки точности используется при численном интегрировании дифференциальных уравнений методами Рунге-Кутта?
Задание № 1. Найти три итерации по методу последовательных приближений решения задачи Коши
Оценить
погрешность y3(x)
в множестве
Варианты задания 1 приводятся в таблице 8.
Таблица 8
Вари анты |
f(x,y) |
x0 |
y0 |
a |
b |
Вари анты |
f(x) |
1 |
xy2-x2 |
4 |
0,7 |
4,5 |
1,5 |
16 |
x2y+1 |
2 |
4x-3y2 |
3 |
0,8 |
3,5 |
2 |
17 |
x2y2 +0,2 |
3 |
4,1x-y2+0,1 |
1 |
3,4 |
1,5 |
4 |
18 |
0,1x2y+2,9 |
4 |
x+2,3y2+2 |
1 |
0,9 |
1,5 |
1,5 |
19 |
0,5xy+2,5 |
5 |
x2 y |
0 |
1,1 |
0,9 |
1,9 |
20 |
2xy2 -x2 |
6 |
x2 y2 |
1 |
1 |
1,9 |
1,7 |
21 |
4,4x-3y2 |
7 |
0,1 x2 y+0,9 |
0 |
2 |
0,5 |
3 |
22 |
5,2x-y2 +0,1 |
8 |
x2+0,5y2 |
0,3 |
0,7 |
1 |
1,2 |
23 |
0,1x3y +2x |
9 |
3,2x2+y2 |
3 |
2 |
3,5 |
2,5 |
24 |
3x2y |
10 |
0,5xy+2 |
0,1 |
2 |
0,5 |
2,6 |
25 |
2x+2,3y2 |
11 |
x3y +2x |
0 |
1 |
0,5 |
1,5 |
26 |
x2+0,8y2 |
12 |
2xy+ x3 |
0,5 |
0,5 |
1 |
1 |
27 |
x3y +3x |
13 |
x3y2 +0,5 x2 |
1 |
0,3 |
1,5 |
0,5 |
28 |
3xy+ x3 |
14 |
0,5x3y2 +3x |
0 |
0 |
1 |
1 |
29 |
2x3y2+x2 |
15 |
4,4x4+0,2xy |
-1 |
-2 |
0,4 |
1,6 |
30 |
2,1y-(x+1)3 |
Задание № 2. Методом Эйлера-Коши и методом Рунге-Кутта четвертого порядка точности проинтегрировать задачу Коши на отрезке [x0, x10] с шагом h и шагом . Оценить погрешность.
Варианты задания 2 приводятся в таблице 9.
Указания к выполнению заданий
Задание № 1. Сначала проверить выполнимость условий теоремы о существовании и единственности решения задачи Коши, найти значения констант M, N и d, которые используются для оценки погрешности.
Таблица 9
Варианты |
f(x,y) |
x0 |
y0 |
h |
Вари анты |
f(x,y) |
x0 |
y0 |
h |
1 |
xy3 -x2 |
4 |
0,7 |
0,01 |
16 |
x+cos
|
-2 |
3 |
0,01 |
2 |
|
2,6 |
1,8 |
0,02 |
17 |
|
0 |
2,9 |
0,02 |
3 |
cos (1,5x-y2)-1,3 |
-1 |
0,2 |
0,02 |
18 |
sin (x+y)+1,5 |
1,5 |
0,5 |
0,01 |
4 |
x2+xy +y2 |
2 |
1,2 |
0,01 |
19 |
x2+0,5y2 +3 |
1 |
2,1 |
0,01 |
5 |
|
0 |
0,3 |
0,05 |
20 |
1,8-sin(x+y)2 |
2,1 |
2,5 |
0,01 |
6 |
cos (1,5y+x)2 +1,4 |
1 |
0,9 |
0,01 |
21 |
0,5y(1-0,5x) |
0 |
1 |
0,01 |
7 |
4,1x -y2 +0,6 |
0,6 |
3,4 |
0,02 |
22 |
|
3 |
1,7 |
0,02 |
8 |
|
1,5 |
2,1 |
0,05 |
23 |
0,1y2(2-x2 ) |
0,2 |
1,3 |
0,01 |
9 |
x+cos
|
2,1 |
2,5 |
0,01 |
24 |
|
0,5 |
0,3 |
0,05 |
10 |
|
3 |
1,7 |
0,02 |
25 |
|
0,1 |
2,5 |
0,02 |
11 |
2,5x+cos(y+0,6) |
1 |
1,5 |
0,02 |
26 |
sin(x2+1,1y)+2 |
1,7 |
0,6 |
0,01 |
12 |
x +2,5y2 +2 |
1 |
0,9 |
0,01 |
27 |
|
1,5 |
2,1 |
0,05 |
13 |
2-sin(x+y)2 |
2 |
2,3 |
0,01 |
28 |
cos (2x-y2)-1,5 |
1,2 |
0,4 |
0,02 |
14 |
|
0,1 |
1,2 |
0,05 |
29 |
|
2,5 |
1,5 |
0,02 |
15 |
|
-2 |
0,5 |
0,02 |
30 |
|
-1 |
1,6 |
0,01 |
-3y2
+1
+2x
-0,4
+2y
+3x2
-0,4
+1
+2y
+x+1
-2y2
Задание № 2. Вычисления записать в таблице. Например, для метода четвертого порядка точности таблица имеет вид:
i |
xi |
yi |
k1( i) |
k2( i) |
k3( i) |
k4( i) |
yi |
yi* |
k1( i)* |
k2( i)* |
k3( i)* |
k4( i)* |
yi* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
причем в первой половине таблицы записываются вычисления с шагом h, а во второй – с шагом .