
- •«Численные методы»
- •Программа курса
- •Лабораторная работа 1 Приближенное решение нелинейных уравнений с одной переменной
- •Контрольные вопросы
- •Лабораторная работа 2 Метод простой итерации
- •Метод простой итерации,
- •Контрольные вопросы
- •Лабораторная работа 3 Интерполирование функций
- •Контрольные вопросы
- •Лабораторная работа 4 Численное дифференцирование и интегрирование
- •Контрольные вопросы
- •Указания к выполнению заданий
- •Лабораторная работа 5 Среднеквадратическое приближение функций и построение эмпирических формул
- •Контрольные вопросы
- •Лабораторная работа 6 Приближенное решение обыкновенных дифференциальных уравнений первого порядка
- •Метод Рунге-Кутта четвертого порядка точности
- •Контрольные вопросы
- •Литература
- •Составители р.А. Шафиев, е.В. Архаров, в.Е. Уваров, и.Ю. Ястребова
- •Подписано в печать Печать трафаретная
- •603950, Н. Новгород, ул. Ульянова, 1
Лабораторная работа 3 Интерполирование функций
Задача интерполирования: пусть в n+1 точках x0, x1, x2,…, xn известны значения функции y=f(x): f(x0)=y0, f(x1)=y1, f(x2)=y2,…, f(xn)=yn. Требуется подобрать достаточно простую функцию F(x), удовлетворяющую условиям: в точках x0, x1, x2,…, xn значения функции F(x) должны совпадать со значениями данной функции f(x), то есть F(xk)= f(xk), k=0, 1, 2, …, n.
При остальных значениях x из области определения будем считать, что выполняется приближенное равенство
f(x) F(x).
Функция F(x) называется интерполирующей, процесс ее построения – интерполированием, а точки x0, x1, x2,…, xn – узлами интерполяции. Часто в качестве функции F(x) берется многочлен Pn(x), который называется интерполяционным многочленом.
Интерполяционный многочлен Лагранжа
Многочлен вида

называется интерполяционным многочленом Лагранжа. Многочлен Лагранжа можно построить для любой таблично заданной функции. Оценка погрешности:
![]()
где
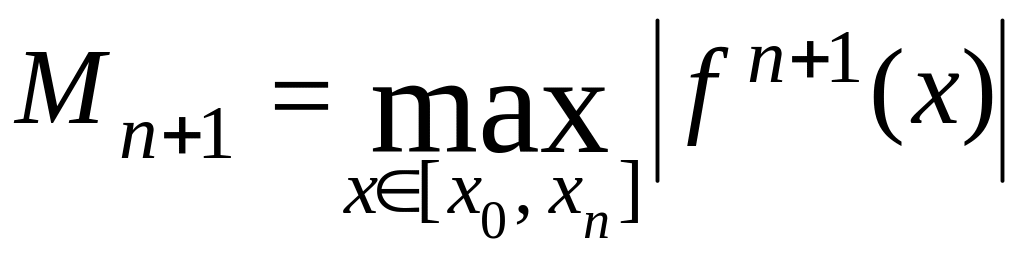 ,
,
![]() .
.
На практике такая оценка погрешности, как правило, оказывается завышенной.
Интерполяционный многочлен Ньютона
Пусть функция y=f(x) задана таблицей с постоянным шагом h:
xi |
x0 |
x1 |
x2 |
… |
xn |
yi |
y0 |
y1 |
y2 |
… |
yn |
где xi=x0+ih, i=1,2,…,n. Такую таблицу называют таблицей с равноотстоящими узлами. Для таблицы с равноотстоящими узлами определяются конечные разности. Конечными разностями первого порядка называются числа, равные приращениям значений функции
y0=y1-y0, y1=y2-y1, …, yn-1=yn-yn-1.
Конечными разностями порядка k, k2 называются числа, определенные равенствами:
kym=k-1ym+1 -k-1ym.
Положим
![]() ,
тогда
,
тогда
![]() ,
,
![]() ,
…,
,
…,
![]() .
Многочлен вида
.
Многочлен вида
![]()
называется
первым интерполяционным многочленом
Ньютона. Его удобно использовать для
нахождения значения таблично заданной
функции в промежуточной точке,
расположенной ближе к началу таблицы,
причем в качестве точки x0
следует
брать ближайший к ней слева узел
интерполяции
![]() и положить
и положить
![]() .
Первый многочлен Ньютона в этом случае
примет вид
.
Первый многочлен Ньютона в этом случае
примет вид
 .
.
Если требуется найти значение таблично заданной функции в точке, расположенной ближе к концу таблицы, то используется второй интерполяционный многочлен Ньютона, который определяется формулой
![]() причем
в качестве xn
следует брать ближайший к точке x
справа узел интерполяции
причем
в качестве xn
следует брать ближайший к точке x
справа узел интерполяции
![]() .
.
Контрольные вопросы
Как ставится задача интерполирования функции?
Как обосновывается существование и единственность интерполяционного многочлена? Как связана его степень с количеством узлов интерполяции?
Как строятся интерполяционные многочлены Лагранжа и Ньютона? В чем особенности этих двух способов интерполяции?
В чем различие в применении первой и второй интерполяционных формул Ньютона?
Какова оценка погрешности интерполяционных формул, если интерполируемая функция задана аналитически? Как изменяется эта оценка, когда функция задана таблично?
Как используется метод интерполирования для уплотнения таблиц функций?
Задание №1. По таблице значений функции
-
x
x0
x1
x2
x3
f(x)
y0
y1
y2
y3
составить интерполяционный многочлен Лагранжа. Построить его график и отметить на нем точки Мi(xi;yi),i=0,1,2,3.
Варианты задания 1 приводятся в таблице 3.
Таблица 3
Вари анты |
x0 |
x1 |
x2 |
x3 |
y0 |
y1 |
y2 |
y3 |
Вари анты |
x0 |
x1 |
x2 |
x3 |
y0 |
y1 |
y2 |
y3 |
1 |
-1 |
0 |
3 |
5 |
-3 |
5 |
2 |
7 |
16 |
-7 |
-5 |
-4 |
0 |
4 |
-4 |
5 |
-2 |
2 |
0 |
2 |
3 |
5 |
2 |
4 |
1 |
7 |
17 |
-1 |
1 |
4 |
9 |
5 |
-2 |
9 |
3 |
3 |
0 |
2 |
3 |
6 |
-1 |
-4 |
2 |
0 |
18 |
7 |
8 |
10 |
13 |
6 |
-2 |
7 |
2 |
4 |
3 |
7 |
9 |
13 |
-4 |
2 |
-2 |
3 |
19 |
-5 |
-4 |
0 |
2 |
7 |
4 |
8 |
-2 |
5 |
-3 |
-1 |
3 |
4 |
7 |
-1 |
4 |
3 |
20 |
-3 |
-1 |
1 |
4 |
11 |
-1 |
6 |
1 |
6 |
-1 |
1 |
2 |
4 |
-5 |
-3 |
-7 |
2 |
21 |
-2 |
0 |
3 |
8 |
8 |
1 |
5 |
-4 |
7 |
-2 |
-1 |
2 |
5 |
4 |
9 |
1 |
7 |
22 |
-3 |
0 |
5 |
8 |
0 |
-4 |
2 |
-9 |
8 |
0 |
2 |
4 |
5 |
3 |
9 |
-3 |
6 |
23 |
-5 |
-3 |
1 |
3 |
2 |
-4 |
1 |
-7 |
9 |
-4 |
-2 |
0 |
3 |
2 |
8 |
5 |
6 |
24 |
-3 |
-1,5 |
1 |
2 |
-1 |
7 |
-4 |
4 |
10 |
-3 |
-1 |
1,5 |
3 |
1 |
4 |
-7 |
1 |
25 |
-5 |
-2 |
0 |
4 |
-1 |
2 |
-8 |
-4 |
11 |
2 |
4 |
7 |
10 |
-1 |
-6 |
3 |
-2 |
26 |
7 |
8 |
10 |
11 |
6 |
-2 |
7 |
0 |
12 |
-10 |
-9 |
-7 |
-4 |
0 |
3 |
-3 |
4 |
27 |
0 |
1 |
2 |
4 |
4 |
7 |
8 |
-1 |
13 |
0 |
1 |
4 |
6 |
7 |
-1 |
8 |
4 |
28 |
-6 |
-3 |
-1 |
3 |
8 |
4 |
9 |
1 |
14 |
-10 |
-8 |
-5 |
0 |
5 |
9 |
-2 |
4 |
29 |
-4 |
2 |
6 |
10 |
5 |
-4 |
3 |
-3 |
15 |
-4 |
-1 |
3 |
8 |
3 |
-5 |
-1 |
7 |
30 |
-5 |
-3 |
3 |
5 |
9 |
2 |
5 |
-1 |
Задание №2. По заданной таблице значений функции вычислить значение этой функции в одном промежуточном значении x с помощью интерполяционного многочлена Лагранжа. Найти значение функции в точке x из ее аналитического выражения и вычислить абсолютную погрешность интерполяции.
Задание №3. Уплотнить часть [a; b] таблицы заданной функции с шагом H , пользуясь интерполяционными формулами Ньютона.
Для отыскания вариантов к заданиям 2 и 3 используется таблица 4.
Таблица 4
Вари анты |
Задание 2 |
Задание 3 |
||||
таблица |
x |
таблица |
a |
b |
H |
|
1 |
4.1 |
3,8 |
4.5 |
0,6 |
0,75 |
0,01 |
2 |
4.2 |
9,5 |
4.6 |
0,15 |
0,3 |
0,01 |
3 |
4.3 |
0,5 |
4.7 |
1,0 |
1,15 |
0,01 |
4 |
4.4 |
4,8 |
4.8 |
0,9 |
1,05 |
0,01 |
5 |
4.1 |
9,1 |
4.5 |
0,7 |
0,85 |
0,01 |
6 |
4.2 |
3,9 |
4.6 |
0,05 |
0,25 |
0,0125 |
7 |
4.3 |
3,3 |
4.7 |
1,0 |
1,2 |
0,0125 |
8 |
4.4 |
4,0 |
4.8 |
0,9 |
1,1 |
0,0125 |
9 |
4.1 |
2,9 |
4.5 |
0,6 |
0,8 |
0,0125 |
Продолжение таблицы 4
Вари анты |
Задание 2 |
Задание 3 |
||||
таблица |
x |
таблица |
a |
b |
H |
|
10 |
4.2 |
5,3 |
4.6 |
0,05 |
0,2 |
0,01 |
11 |
4.3 |
9,1 |
4.7 |
1,1 |
1,25 |
0,01 |
12 |
4.4 |
7,6 |
4.8 |
1,35 |
1,5 |
0,01 |
13 |
4.1 |
4,4 |
4.5 |
1,05 |
1,2 |
0,01 |
14 |
4.2 |
2,5 |
4.6 |
0,25 |
0,4 |
0,01 |
15 |
4.3 |
5,2 |
4.7 |
1,1 |
1,3 |
0,0125 |
16 |
4.4 |
10,8 |
4.8 |
1,1 |
1,25 |
0,01 |
17 |
4.1 |
10,0 |
4.5 |
1,0 |
1,2 |
0,0125 |
18 |
4.2 |
5,6 |
4.6 |
0,5 |
0,65 |
0,01 |
19 |
4.3 |
3,0 |
4.7 |
1,35 |
1,5 |
0,01 |
20 |
4.4 |
3,5 |
4.8 |
1,25 |
1,4 |
0,01 |
21 |
4.1 |
5,8 |
4.5 |
0,95 |
1,1 |
0,01 |
22 |
4.2 |
7,9 |
4.6 |
0,3 |
0,55 |
0,01 |
23 |
4.3 |
2,3 |
4.7 |
1,3 |
1,45 |
0,01 |
24 |
4.4 |
7,0 |
4.8 |
1,0 |
1,2 |
0,0125 |
25 |
4.1 |
8,6 |
4.5 |
0,9 |
1,05 |
0,01 |
26 |
4.2 |
7,0 |
4.6 |
0,3 |
0,45 |
0,01 |
27 |
4.3 |
8,2 |
4.7 |
1,2 |
1,4 |
0,0125 |
28 |
4.4 |
8,5 |
4.8 |
1,2 |
1,35 |
0,01 |
29 |
4.1 |
4,1 |
4.5 |
0,9 |
1,1 |
0,0125 |
30 |
4.2 |
3,5 |
4.6 |
0,1 |
0,25 |
0,01 |
Таблица 4.1 Таблица 4.2 Таблица 4.3 Таблица 4.4
x |
|
|
x |
ln2,3x- |
|
x |
2,1sin0,37x |
|
x |
1,7 -cos(0,4-0,7x) |
1,3 |
1,7777 |
|
1,2 |
0,3486 |
|
-3,2 |
-1,9449 |
|
2,6 |
2,1874 |
2,1 |
4,5634 |
|
1,9 |
1,0537 |
|
-0,8 |
-0,6126 |
|
3,3 |
2,8637 |
3,7 |
13,8436 |
|
3,3 |
1,7844 |
|
0,4 |
0,3097 |
|
4,7 |
3,8161 |
4,5 |
20,3952 |
|
4,7 |
2,2103 |
|
2,8 |
1,8068 |
|
6,1 |
3,8524 |
6,1 |
37,3387 |
|
5,4 |
2,3712 |
|
4,0 |
2,0913 |
|
7,5 |
3,1905 |
7,7 |
59,4051 |
|
6,8 |
2,6322 |
|
6,4 |
1,4673 |
|
8,2 |
2,8409 |
8,5 |
72,3593 |
|
7,5 |
2,7411 |
|
7,6 |
0,6797 |
|
9,6 |
2,6137 |
8,8 |
77,5473 |
|
8,2 |
2,8395 |
|
8,1 |
0,3026 |
|
10,1 |
2,7486 |
9,3 |
86,5941 |
|
8,9 |
2,9291 |
|
8,7 |
-0,1624 |
|
10,9 |
3,1850 |
10,4 |
108,2578 |
|
9,4 |
2,9885 |
|
9,5 |
-0,7661 |
|
11,3 |
3,4776 |
11,0 |
121,0947 |
|
9,8 |
3,0337 |
|
10,2 |
-1,2413 |
|
12,1 |
4,1172 |
Таблица 4.5 Таблица 4.6 Таблица 4.7 Таблица 4.8
x |
sinx |
|
x |
cos x |
|
x |
sin x |
|
x |
cos x |
0,6 |
0,5646 |
|
0,05 |
0,9988 |
|
1,0 |
0,8415 |
|
0,9 |
0,6216 |
0,7 |
0,6442 |
|
0,15 |
0,9888 |
|
1,1 |
0,8912 |
|
1,0 |
0,5403 |
0,8 |
0,7174 |
|
0,25 |
0,9689 |
|
1,2 |
0,9320 |
|
1,1 |
0,4536 |
0,9 |
0,7833 |
|
0,35 |
0,9394 |
|
1,3 |
0,9636 |
|
1,2 |
0,3624 |
1,0 |
0,8415 |
|
0,45 |
0,9004 |
|
1,4 |
0,9854 |
|
1,3 |
0,2675 |
1,1 |
0,8912 |
|
0,55 |
0,8525 |
|
1,5 |
0,9975 |
|
1,4 |
0,1700 |
1,2 |
0,9320 |
|
0,65 |
0,7961 |
|
1,6 |
0,9996 |
|
1,5 |
0,0707 |
Указания к выполнению заданий
Задание №2. Для вычисления значения таблично заданной функции в промежуточной точке явный вид многочлена Лагранжа можно не находить. Вычисления проводить по таблице
i |
0 |
1 |
2 |
… |
n |
pi=(0)(1)…(n) |
yi |
yi /pi |
0 |
x-x0 |
x0-x1 |
x0-x2 |
|
x0-xn |
|
|
|
1 |
x1-x0 |
x-x1 |
x1-x2 |
|
x1-xn |
|
|
|
2 |
x2-x0 |
x2-x1 |
x-x2 |
|
x2-xn |
|
|
|
… |
|
|
|
|
|
|
|
|
n |
xn-x0 |
xn-x1 |
xn-x2 |
|
x-xn |
|
|
|
Далее
следует вычислить
 и
и
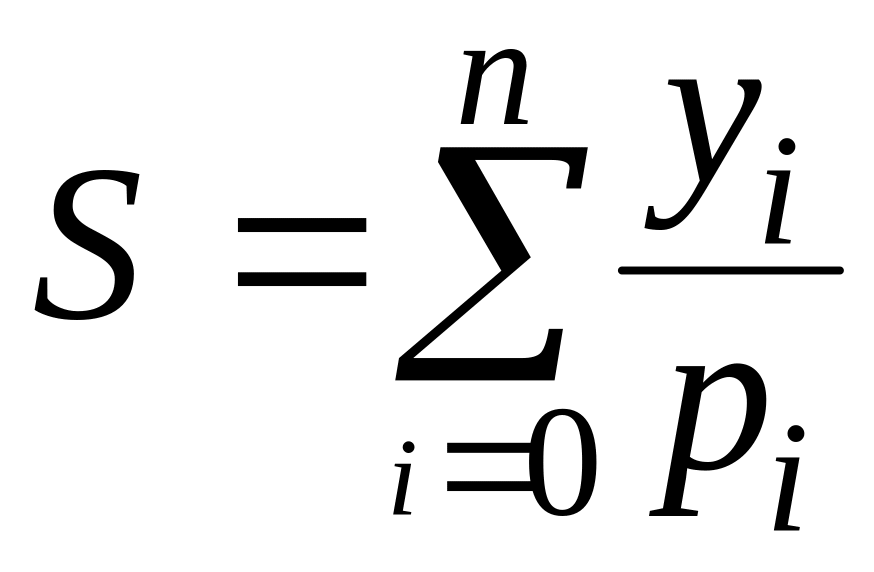 .
Тогда
Ln
(x)
= Пn+1
(x)S.
.
Тогда
Ln
(x)
= Пn+1
(x)S.
Задание №3. Составить таблицу конечных разностей
i |
xi |
yi |
yi |
2 yi |
|
n yi |
0 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
… |
|
|
|
|
|
|
n |
|
|
|
|
|
|
В каждом столбце, начиная с четвертого, будет на одно число меньше, чем в предыдущем.
Результаты вычислений значений функции в промежуточных точках расположить в таблице
-
x
t
Pn (x)
Интерполяционные формулы Ньютона дают хороший результат в случае, когда t[0; 1]. Если внутри отрезка [a; b], на котором требуется уплотнить таблицу, находится узловая точка xi, то на каждом из отрезков [a; xi] и [xi; b] вычисления выполняются отдельно.
