32

Министерство образования Российской Федерации

Нижегородский государственный педагогический

университет

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

ПО КУРСУ

«Численные методы»

Нижний Новгород

2003 г.

Печатается по решению редакционно-издательского совета НГПУ.

Лабораторный практикум по курсу «Численные методы». – Н. Новгород: НГПУ, 2003. – 32 с.

По курсу «Численные методы» предусмотрено выполнение студентами ряда лабораторных работ. Настоящее издание включает описание лабораторных работ по шести темам: приводится краткое содержание теоретического материала, необходимого для выполнения работы, контрольные вопросы, 30 вариантов заданий и указания к выполнению заданий.

Лабораторный практикум предназначен для студентов очного отделения математического факультета.

Составители: Р.А. Шафиев, доктор физ.-мат. наук, проф.

Е.В. Архаров, ст. преподаватель

В.Е. Уваров, аспирант

И.Ю. Ястребова, ст. преподаватель

Рецензент: М.И. Малкин, канд. физ.-мат. наук, доцент каф. мат.анализа НГПУ

Отв. за выпуск: С.Ю. Галкина, канд. физ.-мат. наук, зав. каф. мат.анализа.

Программа курса

1. Понятие об учете погрешностей приближенных вычислений.

2. Приближенное решение уравнений с одной переменной: отделение корней, метод половинного деления, методы хорд и касательных, комбинированный метод. Апостериорные оценки погрешностей методов.

3. Метод простой итерации: обоснование сходимости, оценка точности. Принцип сжимающих отображений в метрических пространствах. Применение к системам линейных и нелинейных уравнений.

4. Интерполирование функций: постановка задачи и ее разрешимость. Вывод интерполяционных формул Лагранжа и Ньютона. Оценка погрешности формул. Кусочно-полиномиальное интерполирование: кубические сплайны.

5. Численное дифференцирование: особенности задачи. Численное дифференцирование на основе интерполяционных формул. Оценка остаточного члена.

6. Численное интегрирование. Квадратурная формула Ньютона-Котеса. Метод трапеций и метод Симпсона. Оценки погрешностей методов.

7. Среднеквадратическое приближение функций: постановка задачи точечной аппроксимации. Многочлен наилучшего среднеквадратического приближения: способ построения, существование и единственность.

8. Способ наименьших квадратов составления эмпирических формул. Линейная, квадратичная, степенная и показательная зависимости.

9. Решение обыкновенных дифференциальных уравнений первого порядка. Применение принципа сжимающих отображений к решению задачи Коши. Метод последовательных приближений. Методы численного интегрирования дифференциальных уравнений типа Рунге-Кутта: метод ломаных Эйлера, метод Эйлера-Коши, метод четвертого порядка точности.

Лабораторная работа 1 Приближенное решение нелинейных уравнений с одной переменной

Рассмотрим нелинейное уравнение общего вида:

f(x)=0, (1)

где f(x) – действительная (достаточно гладкая) функция действительной переменной x.

Поставим задачу приближенного вычисления действительных простых изолированных корней уравнения (1). Корень уравнения (1) называют также нулем функции f(x).

Число  называется простым корнем уравнения (1), если f()=0, но f ' ()0.

Число называется приближенным значением корня  или просто приближенным корнем уравнения (1) с заданной точностью , если | -|<.

Отрезок [a; b] называется промежутком изоляции корня , если на нем, кроме , нет корней уравнения (1).

Решение поставленной задачи разбивается на два этапа. I этап – отделение корней, то есть установление промежутков изоляции корней. На этом этапе полезны следующие утверждения из анализа: если

1. f(x) непрерывна на [a; b],

2. f(a) f(b)<0,

то уравнение (1) имеет корень [a; b]; если дополнительно

3. f ' (x) сохраняет знак на [a; b],

то [a; b] – промежуток изоляции корня .

Пусть найден отрезок [a; b], где f(a) f(b)<0, который содержит только один корень уравнения (1). Этот неизвестный корень обозначим буквой . На II этапе по заданному числу  >0 требуется на отрезке [a; b] найти приближенный корень с точностью . Корень будем искать итерационными методами.

Метод половинного деления

состоит в повторении (итерировании) следующей процедуры:

1. вычисление точки , соответствующей середине отрезка [a; b];

2. вычисление значения функции f(c);

3. переход к отрезку удовлетворяющему всем свойствам отрезка [a; b], но вдвое меньшей длины.

В результате получаем последовательность {c_n} середин отрезков [a_n; b_n], длина которых неограниченно уменьшается.

"Правило останова": вычисления прекращаются, когда впервые либо f(c_n)=0, либо b_n - a_n  2. Искомый приближенный корень

.

Метод хорд

состоит в построении последовательности {x_n} по итерационной формуле

x_n+1=x_n- ( ₀-x_n), n=0,1,2,…,

начиная из начального приближения

x₀= (2)

а ₀ – противоположный x₀ конец отрезка [a; b].

Условие сохранения знака f '' (x) на отрезке [a; b] является достаточным условием сходимости метода хорд. Если f ' (x) сохраняет знак на отрезке [a; b] и выполняется условие

0 < m₁  | f ' (x)|  M₁, x[a; b],

то имеет место следующее

"правило останова": вычисления прекращаются, когда впервые удовлетворяется неравенство

.

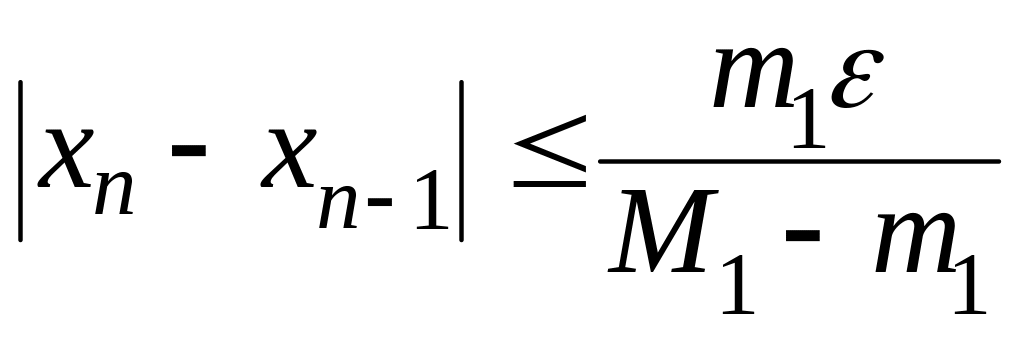Искомый приближенный корень

= x_n.

Метод Ньютона (метод касательных)

состоит в построении последовательности (черта над x_n ставится для удобства изложения) по итерационной формуле

, n=0,1,2,…,

начиная из начального приближения ₀, определенного в методе хорд (2).

Условие сохранения знаков f ' (x) и f '' (x) на отрезке [a; b] является достаточным условием сходимости метода Ньютона. Если вторая производная f '' (x) ограничена на отрезке [a; b] и выполняется условие

0 < m₁  | f ' (x)|, x[a; b],

то имеет место следующее

"правило останова": вычисления прекращаются, когда впервые удовлетворяется неравенство| _n- _n-1|  .

Искомый приближенный корень

= _n.

Комбинированный метод

состоит в построении двух последовательностей {t_n} и путем поочередного применения итерационных формул

начиная из начальных приближений

t₀ = x₀, ₀ = ₀,

где x₀, ₀ - концы отрезка [a; b], определенные в (2).

Поясним комбинированный метод на рисунке.

"Правило останова": вычисления прекращаются, когда впервые удовлетворяется неравенство

| t_n - _n|  2.

Искомый приближенный корень

.