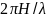36. Морські хвилі. Короткі, довгі хвилі та хвилі кінцевої глибини. Енергія хвиль.
Перша теорія хвиль (трохоідальна теорія)
Для початку слід запам’ятати, що хвиля — це форма, що рухається, а вода при цьому залишається на місці.
Частинки води у хвилі рухаються по колу (майже замкнута колова орбіта), діаметр якого дорівнює висоті хвилі; причому, частинки, які знаходяться в гребені, рухаються в напрямку переміщення, хвилі, а ті, що знаходяться в підошві - в протилежному напрямку (рис.6.1).
Профіль хвилі найближчий до трохоїди - кривої, яку описує точка в середині кола, коли коло рухається прямо.
Гребені і підошви хвиль на глибині розміщуються під гребенями і підошвами на поверхні, тобто ні довжина(λ), ні період(τ), а значить і фазова швидкість(Сф) хвиль з глибиною не змінюється.
Колові орбіти дуже швидко зменшуються з глибиною, тобто, хвилі швидко затухають (за експоненційною залежністю).
На глибині, що дорівнює довжині хвилі - хвиль немає; а на глибині Z= 0,5λ їх висота приблизно рівна 0,04h0 (h0 - висоті хвилі на поверхні), тобто дуже маленька. Таким чином, можна вважати, що на глибині половини довжини хвилі, хвилювання практично відсутнє.
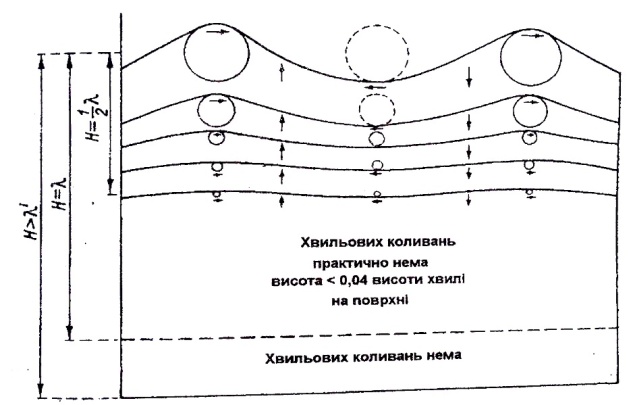
Рис. 6.1Зміна профілю трохоїдальної хвилі з глибиною. Гребені та підошви хвиль на глибині розташовані під гребенями та підошвами на поверхні, тобто ні довжина (λ) ні період (τ), а отже, і фазова швидкість (Сф) хвиль з глибиною не змінюються. На глибині, що дорівнює половині довжини хвилі, хвилювання практично відсутнє.
Якщо глибина моря набагато менша половини довжини хвилі, орбіти руху часток води сплющуються, а біля дна рух стає майже реверсно — поступальним (рис.6.4).
Енергія трохоїдальної хвилі (ідеальної) складається з кінетичної та потенційної, які рівні між собою.Всередньому енергія за період, зосереджена під одиничною площею поверхні хвилі (питома енергія) буде рівна
де ρ — густина морської води, g — прискорення вільного падіння,h — висота хвилі.
Повна ж енергія хвилі певних розмірів буде результатом множення питомої на площу поверхні цієї хвилі:
де b - ширина гребеня; λ - довжина хвилі.
ДОДАТКОВИЙ МАТЕРІАЛ
Морські хвилі класифікуються за різними ознаками. Наведемо деякі із загально прийнятих класифікацій.
1.В залежності від сил, що викликають їх (вітрові, анемобаричні, сейсмічні, припливні, корабельні та ін.)
2. Вільні та вимушені (знаходяться. весь час під дією сили, що збудила їх, чи ні).
3. За місцем знаходження (поверхневі та внутрішні).
4. За характером руху (поступальні, коли форма хвилі рухається у просторі, чи стоячі — коли форма стоїть на місці) та ін.
Хвилі можуть бути будь-яких розмірів: починаючи від мілких брижів і закінчуючи гігантськими штормовими та припливними хвилями, довжина яких теоретично дорівнює половині довжини Земної кулі. Та існує єдина система позначення основних елементів хвиль (рис 6.2 ):
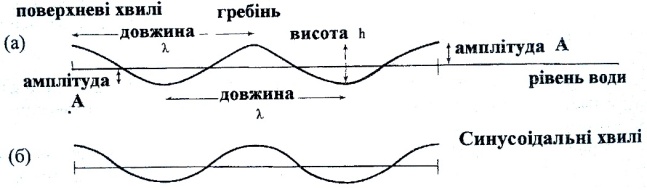
Рис. 6.2 Профіль трохоїдальної (ідеальної) хвилі (а), синусоїдальної хвилі (б).
гребінь — найвища точка хвилі;
улоговина (підошва) — найнижча точка хвилі;
висота хвилі (h) — відстань по вертикалі від улоговини до гребеня;
довжина хвилі (λ) — відстань по горизонталі між двома послідовними гребенями (або улоговинами);
період хвилі (τ) – проміжокчасу в секундах між моментами проходження через одну і ту саму точку двох послідовних гребенів хвилі (або час, за який проходить одна довжина хвилі);
фазова швидкість хвилі (Сф = λ/τ)— швидкість переміщення гребеня хвилі за її період (фазова - бо рухається лише форма, вода при цьому залишається на місці);
крутизна хвилі - співвідношення висоти до довжини хвилі (h/λ); якщо це співвідношення буде дорівнювати 1 до 7 (що рівно приблизно куту 120°під гребенем хвилі) - то хвиля повинна зруйнуватися (рис.6.3);
- ω - кутова швидкість руху часток за орбітами (ω = 2π/τ);
- ν - лінійна швидкість орбітального руху часток (ν = ωr);
- λ = 2πr - довжина хвилі через радіус руху часток в трохоїді;
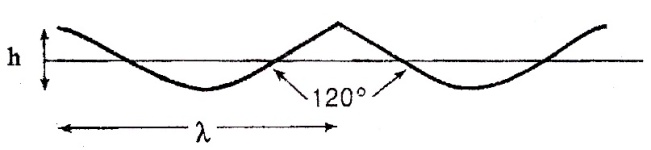
Рис.6.3. Співвідношення висоти до довжини хвилі (1:7) чи відповідний кут 120°, при якому хвиля руйнується.
Якщо глибина моря дуже мала порівняно з довжиною хвилі, тертя об дно деформує орбіти руху частинок води. Дно не дає можливості розвитку вертикальних коливань, тому колові орбіти розтягуються в еліпсоподібні. А біля самого дна рух часток може навіть бути реверсно — поступальний (рис.6.4).
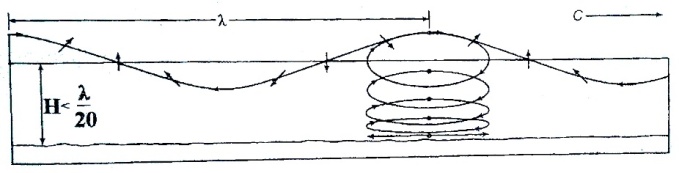
Рис.6.4. Зміна орбіти руху часток води у мілкому морі (Н<<λ/2).
Саме такий рух формує на дні біля самого берега хвилі з піску. Заміривши відстань між двома найближчими пісковими гребенями можна дізнатись довжину хвилі, що сформувала їх.
З формули залежності зміни радіуса орбіти руху часток (r) від глибини (z) та довжини хвилі (λ)
можна зробити висновок, що чим менша глибина і більша довжина хвилі, тим менше повинен змінюватись радіус орбіти і тим більша буде відстань між гірками з піску на дні.
Вплив глибини моря на фазову швидкість хвилі
Перед тим як перейти до цього важливого питання, необхідно чітко розуміти, що є хвилі, які відчувають тертя об дно. Це можливо у тому випадку, коли глибина моря менша від половини довжини хвилі, адже за даними експериментів нижче цього рівня хвилі вже немає. Виходить, що глибина моря через тертя може впливати не тільки на форму орбіти часток у хвилі, а й на швидкість її розповсюдження. Якщо глибина моря велика відносно довжини хвилі, - то звичайно ж цього впливу на швидкість хвилі не буде. Тому вчені розділили (або класифікували) всі хвилі, що спостерігаються в Океані на ті, що відчувають дно; ті, які цього впливу не мають, та ті, на швидкість яких вплив тертя об дно вирішальний.
Хвилі, що рухаються в басейні, глибина якого більша половини довжини хвилі, не відчувають дно і називаються короткими.
Хвилі, що рухаються в басейні, глибина якого менша однієї десятої довжини хвилі, тобто тертя об дно для їх руху є вирішальним, називаються довгими.
Хвилі, що рухаються в басейні, глибина якого менша за половину довжини хвилі, але більша за одну десяту, називаються хвилями мілини. Вплив тертя об дно для їх руху не вирішальний, але відчутний.
Теорія хвиль з урахуванням глибини моря дає наступну формулу для фазової швидкості хвилі:
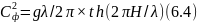
де Н - глибина моря.
Але
ми вже знаємо, що існують хвилі, які
відчувають дно, тобто на швидкість їх
розповсюдження повинно якимсь чином
впливати тертя об дно, та хвилі - вільні
від цього впливу. Скористаємося таблицею
6.1. В ній представлені результати
розрахунків значень тангенсу
гіперболічного
та його аргументу
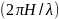при різних співвідношеннях довжини
хвилі до глибини басейну (
),
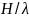в якому вона розповсюджується.
Таблиця 6.1
|
1,0 |
0,5 |
0,25 |
0,12 |
0,10 |
0,05 |
0,016 |
|
6,28 |
3,14 |
1,57 |
0,78 |
0,63 |
0,31 |
0,10 |
|
1,0 |
1,0 |
0,91 |
0,65 |
0,56 |
0,29 |
0,10 |
Як видно з таблиці, для коротких хвиль (де глибина більша 0,5λ, тобто від 0,5; 1,0 і т.д.) значення дорівнює одиниці. Таким чином, загальна формула (6.4) для коротких хвиль перетворюється у дуже просту формулу (6.5), з якої видно, що швидкість хвиль, які не відчувають дно, тобто розповсюджуються в басейні, глибша якого більша половини їх довжини, залежить виключно від довжини хвилі:
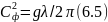
або
Для довгих хвиль (де глибина менша 0,1λ), як видно з таблиці, значення тангенсу гіперболічного практично дорівнює його аргументу . Таким чином, використовуючи формулу (6.4) та замінюючи в ній тангенс гіперболічний на його аргумент, одержуємо, що швидкість довгих хвиль (Н <0,1λ.), тобто хвиль, що рухаються в мілкому басейні відносно їх довжини, визначається виключно глибиною басейну (Н):
Для хвиль мілини (0,5λ> Н >0,1λ) при розрахунках фазової швидкості хвилі користуються загальною формулою (6.4).
Можна зробити висновок, що всі хвилі при підході до похилого берега стають довгими, тому їх швидкість визначається виключно глибиною басейну. Тертя об дно часток води, що рухаються в довгій хвилі, настільки велике, що вони розмивають дно, переміщують величезні маси наносів, змінюючи дно та береги.