14. Теорема про середнє в інтегралі Рімана

Якщо функція f(x) неперервна на [a, b], то

|

Неперервна функція f(x)є інтегрованою на [a, b], за теоремою Вейєрштраса f(x) на [a, b] приймає своє найбільше(найменше) значення

M x [a, b] m= x [a, b]

Тобто

Тобто для f(x) має місце ТЕОРЕМА ПРО ОЦІНКУ

15. Інтеграл зі змінною верхнею границею: означення і неперервність інтегралу зі змінною верхнею границею.

f(x) інтегр. [a,b], що для будь-якого з цього відрізка [a,b] x існує , що являє собою функцію від х. Такий інтеграл, називається інтеграл зі змінною верхньою границею.

Теорема про неперервність інтегралу зі змінною верхньою границею:

Якщо f(x) є інтегрованою на [a,b], то функція є неперервною на [a,b].

Доведення:

Аргументу х надаємо приріст так, щоб т. х+ не вийшла за межі

( .

При цьому F(x) одержимо приріст:

F (x+ , а приріст

Оцінимо , де

Отже, при , а це свідчить про неперервність функції F(x).

16. Диференціювання інтегралу зі змінною верхньою границею.

Теорема Барроу про диференційованість інтегралу зі змінною верхньою границею:

Якщо функція f(x) неперервна на відрізку [a,b], то

F(x) = [a,b] і має місце формула:

F¢(x) = [ = f(x).

Похідна від інтегралу зі змінною верхньою змінною границею = підінтегральній функції на верхній границі.

Доведення:

Розглянемо F¢(x) = ´ =

´f(x) x = f(x).

17. Теорема Ньютона-Лейбніца.

(про обчислення визначеного інтегралу): якщо f(x) неперервна на [a,b], а (х) – будь-яка її первісна, то (b) - .

Доведення:

f(x) непер., то F(x) = є її первісною, бо F¢(x) = f(x) "xÎ [a,b]

Так, як Fі відрізняються на сталу, то F(x) =

Тобто

При x=a Þ 0= Þ C= -

При x=bÞ

Т.ч. обчислення визначеного інтегралу зводиться до знаходження первісної.

18. Заміна змінної у визначеному інтегралі Рімана. Інтеграл Рімана від парної та непарної функції на симетричному проміжку.

Теорема. Якщо функція y=f(x) неперервна на [a,b], x= неперервна з на [ - первісна для f(x) на [a,b], то F ( є первісною для f (

• Якщо функція f(x) [-a,a] і функція є парною f(-x)= f(x)

• f(x) непарна [-a,a]

f(-x)= -f(x)

19. Невласні інтеграли І-го роду: означення, ознака порівняння.

Означення: невласним інтегралом 1-го роду називають при => .

• якщо ця границя існує і скінченна, то цей називають збіжним.

• якщо ця границя не існує ( 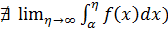чи = 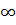, то інтеграл розбіжнй .

Аналогічно визначається інтеграл з нижньою границею, на проміжку (-

=

У випадку визначення на функції f(x) за означенням:

• якщо кожен з них збігається то інтеграл збіжний, якщо розбігається – розбіжний.

Теорема 1.(ознака порівняння)

• якщо функції f(x) та g(x):

1. визначенні і неперервні для

2. 0

• тоді :

1. із збіжності інтеграла

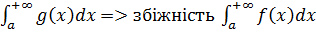
2. із розбіжності інтеграла

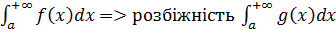
Наслідок.

Якщо в умовах теореми існує

1. якщо 0 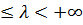, то зі збіжності .

2. якщо .

3. якщо