
- •Понятие числового ряда. Сходимость ряда. Необходимый признак сходимости. Эталонные ряды. Гармонический, обобщенный гармонический и геометрический ряды.
- •Признаки сравнения знакоположительных рядов. Признаки Даламбера и Коши. Предельный признак сравнения рядов. Интегральный признак сходимости рядов.
- •Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимость рядов.
- •Функциональные ряды. Степенные ряды. Признак равномерной сходимости функционального ряда.
- •Область сходимости степенного ряда. Теорема Абеля. Формула для нахождения радиуса сходимости и ее разновидности. Свойства степенных рядов
- •Интегрирование и дифференцирование рядов.
- •Разложение функции в ряд Тейлора. Биномиальный ряд.
- •Разложение функций в ряд Маклорена. Разложение функции .
- •Вычисление интегралов с помощью рядов.
- •Интегрирование дифференциальных уравнений с помощью рядов.
- •Условия разложения функции в ряд Фурье.
- •Условия Дирихле разложения функции в ряд Фурье.
- •Особенности разложения в ряд Фурье нечетных функций.
- •Особенности разложения в ряд Фурье четных функций.
- •Разложение функций в ряд Фурье, заданных на половине периода.
- •Ряд Фурье по ортогональной системе функций.
- •Общие правила составления дифференциального уравнения в задаче с физическим смыслом.
- •Общие правила составления дифференциального уравнения в задаче с геометрическим смыслом.
- •Нелинейное дифференциальное уравнение колебаний математического маятника (качественное описание).
- •Дифференциальное уравнение свободных колебаний груза на пружине.
- •Условие существования и геометрический смысл двойного интеграла.
- •Геометрический смысл двойного интеграла
- •Условие существования и геометрический смысл тройного интеграла.
- •Криволинейные интегралы по замкнутому контуру. Формула Грина.
- •Формула Остроградского-Гаусса.
- •Циркуляция векторного поля. Формула Стокса.
- •Дивергенция и ротор векторного поля.
- •Дивергенция
Криволинейные интегралы по замкнутому контуру. Формула Грина.
Криволинейным
интегралом II рода от
функций ![]() и
и ![]() по
плоской кривой
по
плоской кривой ![]() от
точки
от
точки ![]() к
точке
к
точке ![]() называют
предел ,
называют
предел ,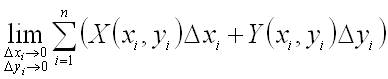 где
точки
где
точки ![]() –
точки, которые разбивают участок
кривой
от
точки
до
точки
на
–
точки, которые разбивают участок
кривой
от
точки
до
точки
на ![]() частей,
а
частей,
а ![]() и
и ![]() –
приращения соответствующих координат
при переходе от точки
к
точке
–
приращения соответствующих координат
при переходе от точки
к
точке ![]() .
Криволинейный интеграл II рода
обозначают:
.
Криволинейный интеграл II рода
обозначают:
![]() или
или 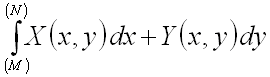 .
Направление
по кривой
от
точки
до
точки
называется направлением
интегрирования.
Если
кривая
пространственная,
то криволинейный интеграл II рода от
трех функций
.
Направление
по кривой
от
точки
до
точки
называется направлением
интегрирования.
Если
кривая
пространственная,
то криволинейный интеграл II рода от
трех функций ![]() ,
, ![]() ,
, ![]() определяется
аналогично:
определяется
аналогично:
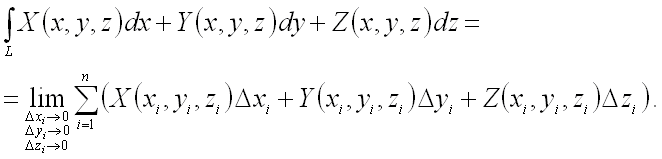
Формула Грина
Пусть
в плоскости ![]() дана
ограниченная замкнутым контуром
правильная
область
дана
ограниченная замкнутым контуром
правильная
область ![]() ,
причем ее проекцией на ось
,
причем ее проекцией на ось ![]() является
отрезок
является
отрезок ![]() ,
снизу область
ограничена
кривой
,
снизу область
ограничена
кривой ![]() ,
а сверху – кривой
,
а сверху – кривой ![]() (в
совокупности эти кривые составляют
замкнутый контур
).
Пусть
также в области
заданы
непрерывные функции
и
,
имеющие непрерывные частные
производные.
Тогда, если обход
контура
совершается
против часовой стрелки, справедлива
следующая формула:
(в
совокупности эти кривые составляют
замкнутый контур
).
Пусть
также в области
заданы
непрерывные функции
и
,
имеющие непрерывные частные
производные.
Тогда, если обход
контура
совершается
против часовой стрелки, справедлива
следующая формула:
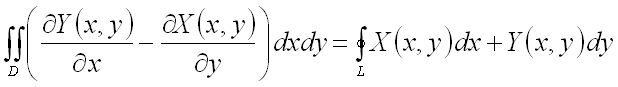 .
.
Криволинейные интегралы первого и второго рода.
Криволинейный интеграл первого рода
Свойства
Линейность:
![]()
Аддитивность: если
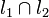 в
одной точке, то
в
одной точке, то
![]()
Монотонность: если
 на
на 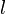 ,
то
,
то
![]()
Теорема о среднем для непрерывной вдоль функции :
![]()
Очевидно,
что: ![]() .
.
5.
Изменение направления обхода кривой
интегрирования не влияет на знак
интеграла: ![]() .
.
6. Криволинейный интеграл первого рода не зависит от параметризации кривой.
Вычисление
Пусть
—
гладкая, спрямляемая кривая, заданная
параметрически (как в определении).
Пусть функция ![]() определена
и интегрируема вдоль кривой
в
смысле криволинейного интеграла первого
рода. Тогда
определена
и интегрируема вдоль кривой
в
смысле криволинейного интеграла первого
рода. Тогда
![]() .
.
Здесь
точкой обозначена производная по ![]() :
: ![]() .
.
Криволинейный интеграл второго рода
Свойства
1. Линейность:
![]()
2. Аддитивность:
![]()
3. ![]()
Замечание. Для криволинейных интегралов второго рода несправедливы свойство монотонности, оценка модуля и теорема о среднем.
Вычисление
Пусть — гладкая, спрямляемая кривая, заданная параметрически (как в определении). Пусть функция определена и интегрируема вдоль кривой в смысле криволинейного интеграла второго рода. Тогда
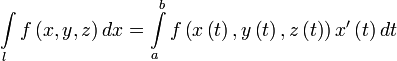 ,
,
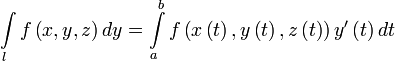 ,
,
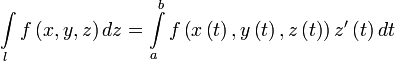 .
.
Если
обозначить за ![]() единичный
вектор касательной к кривой
,
то нетрудно показать, что
единичный
вектор касательной к кривой
,
то нетрудно показать, что
![]()
![]()
![]()
Формула Остроградского-Гаусса.
Формула Остроградского-Гаусса — математическая формула, которая выражает поток векторного поля через замкнутую поверхность интегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью:
![]()
то
есть интеграл
от дивергенции векторного поля ![]() ,
распространённый по некоторому объёму
,
равен потоку вектора
через поверхность
,
ограничивающую данный объём.
,
распространённый по некоторому объёму
,
равен потоку вектора
через поверхность
,
ограничивающую данный объём.
Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности.
В работе Остроградского формула записана в следующем виде:
![]()
где ![]() и
и ![]() —
дифференциалы объёма и поверхности
соответственно. В современной записи
—
дифференциалы объёма и поверхности
соответственно. В современной записи ![]() —
элемент объёма,
—
элемент объёма, ![]() —
элемент поверхности.
—
элемент поверхности. ![]() —
функции, непрерывные вместе со своими
частными производными первого порядка
в замкнутой области пространства,
ограниченного замкнутой гладкой
поверхностью.
—
функции, непрерывные вместе со своими
частными производными первого порядка
в замкнутой области пространства,
ограниченного замкнутой гладкой
поверхностью.
Обобщением формулы Остроградского является формула Стокса для многообразий с краем
