15. Разложение функций в ряд Фурье, заданных на половине периода.

Для разложения этой функции в ряд Фурье достаточно ее доопределить (продолжить) в интервале [–l, 0] произвольным способом так, чтобы образовавшаяся в интервале [–l, l] функция F(x), совпадающая с f(x) на интервале [0, l], удовлетворяла условиям основной теоремы (Дирихле).

Разложив функцию F(x) в ряд Фурье, получим ряд, представляющий в интервале [0, l] заданную функцию f (x). Для нас не имеет значения, что на интервале [–l, 0] это ряд будет представлять другую функцию, по существу не связанную с f (x).

Так как функцию f (x) можно продолжить в [–l, 0] произвольным способом, то можно составить сколько угодно сходящихся тригонометрических рядов, представляющих на интервале [0, l] одну и ту же заданную функцию f (x), а на интервале [–l, 0] самые разнообразные функции (продолжения).

Наиболее целесообразно функцию f (x) доопределить так, чтобы ее значения в точках интервала [–l, 0] находились из условия f (x) = f (–x), т.е. график функции f(x) продолжить симметрично относительно оси Oy, или из условия f (x)= –f (–x) – график функции продолжить симметрично относительно начало координат (продолжить нечетно). В первом случае функция F(x) на интервале [–l, l] будет четной и ряд будет состоять только из косинусов, а во втором – нечетной и ряд будет состоять только из одних синусов.

16. Ряд Фурье по ортогональной системе функций.

Последовательность функций   непрерывных на отрезке [a,b], называется ортогональной системой функции на отрезке [a,b], если все функции последовательности попарно ортогональны на этом отрезке, т. е. если  

Система называется ортогональной и нормированной (ортонормированной) на отрезке [a,b],

если выполняется условие

Пусть теперь f(x) - любая функция непрерывная на отрезке [a,b]. Рядом Фурье такой функции f(x) на отрезке [a,b] по ортогональной системе называется ряд:

коэффициенты которого определяются равенством: 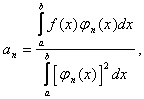 n=1,2,...

Если ортогональная система функций на отрезке [a,b] ортонормированная, то в этом случаи  

 где n=1,2,...

Пусть теперь f(x) - любая функция, непрерывная или имеющая конечное число точек разрыва первого рода на отрезке [a,b]. Рядом Фурье такой функции f(x) на томже отрезке

по ортогональной системе называется ряд: ,

Если ряд Фурье функции f(x) по системе (1) сходится к функции f(x) в каждой ее точке непрерывности, принадлежащей отрезку [a,b]. В этом случае говорят что f(x) на отрезке [a,b] разлагается в ряд по ортогональной системе

17. Общие правила составления дифференциального уравнения в задаче с физическим смыслом.

18. Общие правила составления дифференциального уравнения в задаче с геометрическим смыслом.

19. Нелинейное дифференциальное уравнение колебаний математического маятника (качественное описание).

Дифференциальное уравнение колебаний

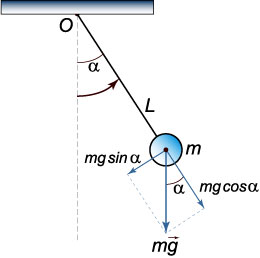
Математический маятник представляет собой идеальную модель, в которой материальная точка массой mподвешена на невесомой и нерастяжимой нити длиной L. В такой системе происходят периодические колебания, которые можно рассматривать как вращение маятника вокруг оси O (рисунок 1).

Рис.1		Рис.2

Динамика вращательного движения описывается дифференциальным уравнением

где ε − угловое ускорение, M − момент силы, вызывающий вращение, I − момент инерции тела относительно оси вращения.  В нашем случае момент силы определяется проекцией силы тяжести на тангенциальное направление, т.е.

Знак минус означает, что при положительном угле поворота α (против часовой стрелки) момент сил вызывает вращение в противоположном направлении.  Момент инерции маятника выражается формулой

Тогда уравнение динамики принимает вид:

В случае малых колебаний полагают sin α ≈ α. В результате возникает линейное дифференциальное уравнение

где 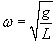  − круговая частота колебаний.  Период малых колебаний маятника описывается известной формулой

Однако при увеличении амплитуды колебаний линейная формула перестает быть справедливой. В этом случае для корректного описания колебательной системы нужно решать исходное нелинейное дифференциальное уравнение.

Период колебаний нелинейного математического маятника

Итак, пусть маятник описывается нелинейным дифференциальным уравнением второго порядка

Будем рассматривать колебания при начальных условиях

Угол α₀ представляет собой амплитуду колебаний.  Порядок уравнения можно понизить, если подобрать подходящий интегрирующий множитель. Умножим данное уравнение на интегрирующий множитель  . Это приводит к уравнению

После интегрирования получаем дифференциальное уравнение первого порядка:

С учетом начальных условий находим постоянную C:

Тогда уравнение принимает вид:

Далее применим тригонометрическую формулу двойного угла

что приводит к следующему дифференциальному уравнению:

Интегрируя это уравнение, получаем

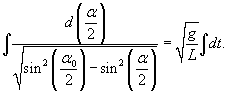
Обозначим 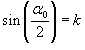  и введем новую переменную θ вместо угла α:

Тогда

Отсюда следует, что

В новых обозначениях наше уравнение записывается как

Обсудим пределы интегрирования. Прохождение маятником дуги от нижней точки α = 0 до максимального отклонения α = α₀ соответствует четверти периода колебаний T/4. Из соотношения между углами α и θследует, что при α = α₀ должно быть sin θ = 1 или θ = π/2. Поэтому получаем следующее выражение для периода колебаний маятника:

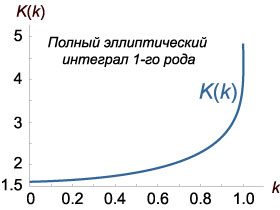
Интеграл в правой части не выражается через элементарные функции. Он представляет собой так называемый полный эллиптический интеграл 1-го рода:

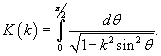
Функция K(k) вычисляется в большинстве математических пакетов. Ее график приведен выше на рисунке 2. Функцию K(k) можно представить также в виде степенного ряда:

где двойные факториалы (2n − 1)!! и (2n)!! обозначают произведение, соответственно, натуральных нечетных и четных чисел.  Заметим, что если мы ограничимся нулевым членом разложения, полагая K(k) ≈ π/2, то получим известную формулу для периода малых колебаний маятника:

Последующие члены ряда при n ≥ 1 как раз позволяют учесть ангармонизм колебаний маятника и нелинейную зависимость периода T от амплитуды колебаний α₀.