6. Интегрирование и дифференцирование рядов.

Рассмотрим степенной ряд 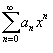 , имеющий радиус сходимости R > 0:

Функция 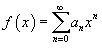  является непрерывной функцией при |x| < R. Степенной ряд внутри интервала сходимости можно дифференцировать почленно. При этом производная степенного ряда выражается формулой

Степенной ряд можно также почленно интегрировать на отрезке, который расположен внутри интервала сходимости. Следовательно, если − R < b < x < R, то выполняется равенство

Если ряд интегрируется на отрезке [0; x], то справедлива формула:

7. Разложение функции в ряд Тейлора. Биномиальный ряд.

Пусть функция   бесконечно дифференцируема в некоторой окрестности точки  . Формальный ряд

называется рядом Тейлора функции   в точке  .

Формула Тейлора

Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции вокрестности некоторой точки.

Теорема:

• Пусть функция   имеет 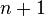  производную в некоторой окрестности точки  , 

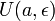
• Пусть 

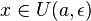
• Пусть 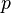  — произвольное положительное число,

тогда:   точка   при   или   при  :

БИНОМИАЛЬНЫЙ РЯД - степенной ряд вида

где n - целое, а α - произвольное фиксированное число (вообще говоря, комплексное), z = x + iy - комплексное переменное, (^α_n) - биномиальные коэффициенты. Для целых α = m ≥ 0 Б. р. сводится к конечной сумме m + 1 слагаемых

называемой Ньютона биномом. 

8. Разложение функций в ряд Маклорена. Разложение функции .

 Разложение функции f(x) в ряд Тейлора при x₀=0   называется разложением этой функции в ряд Маклорена.

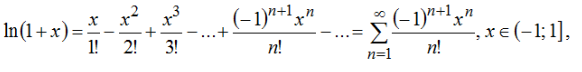
9. Вычисление интегралов с помощью рядов.

Существуют определённые интегралы, которые, как функции верхнего предела, не выражаются в конечном виде через элементарные функции. Такие интегралы иногда бывает удобно вычислять с помощью рядов, т. е. подынтегральная функция представляется в виде разложения в степенной ряд Маклорена:

                   

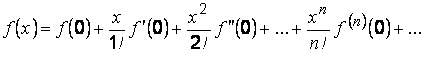
10. Интегрирование дифференциальных уравнений с помощью рядов.

Решения многих дифференциальных уравнений не выражаются в элементарных функциях. В этих случаях пользуются приближенными методами интегрирования дифференциальных уравнений. Одним из таких методов является представление решения уравнения в виде степенного ряда; сумма конечного числа членов этого ряда будет приближенно равна искомому решению. Указанный степенной ряд находят способом неопределенных коэффициентов или способом, основанным на применении ряда Тейлора (Маклорена).

Способ неопределенных коэффициентов особенно удобен в применении к линейным уравнениям, т. е. уравнениям вида

и состоит в следующем.

Если все коэффициенты этого уравнения и свободный член разлагаются в ряды по степеням , сходящиеся в интервале , то искомое решение также представляется степенным рядом

сходящимся в этом же интервале. Подставляя в уравнение функцию и ее производные, приравнивают коэффициенты при одинаковых степенях из полученных при этом уравнений и заданных начальных условий находят коэффициенты

Способ основанный на применение ряда Тейлора (Маклорена), заключается в последовательном дифференцировании данного уравнения. Это дает возможность найти значения производных, входящих в выражения для коэффициентов ряда

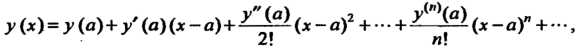
Являющегося решением уравнения.