Экзаменационные вопросы для 2 курса ФВТШС

1. Понятие числового ряда. Сходимость ряда. Необходимый признак сходимости. Эталонные ряды. Гармонический, обобщенный гармонический и геометрический ряды.

Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда). Пусть   — числовая последовательность; рассмотрим наравне с данной последовательностью последовательность , каждый элемент которой представляет собой сумму некоторых членов исходной последовательности. В наиболее простом случае используются обычные частичные суммы вида: Вообще, для обозначения ряда используется символ: , поскольку здесь указана исходная последовательность элементов ряда, а также правило суммирования.

Частной суммой числового ряда   называется сумма  . Числовой ряд называется сходящимся, если существует предел  , при этом   называется суммой ряда.

Необходимый признак сходимости ряда

Если ряд сходится, то   un=0. Доказательство. Пусть ряд u1+u2+…+un… сходится, то есть существует конечный предел  =S. Тогда имеет место также равенство  =S, так как при n  и (n-1) . Вычитая почленно из первого равенства второе, получаем  -  =  = un=0, что и требовалось доказать. Следствие. Если  un≠0, то ряд u1+u2+…+un… расходится.

Эталонные ряды- это ряд, сходимость которого нам известна

Геометрический ряд

Обобщеный гармонический ряд 

В частности, при к=1 получаем гармонический ряд 

2. Признаки сравнения знакоположительных рядов. Признаки Даламбера и Коши. Предельный признак сравнения рядов. Интегральный признак сходимости рядов.

Признаки сравнения знакоположительных рядов.

                            − знакоположительные ряды.

Общий признак сравнения (ОПС). Пусть  . В этом случае:

1. ряд  Q сходится 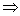   ряд Р  сходится.

2. ряд  Р  расходится    ряд Q расходится.

{ По условию  P_n ≤ Q_n . (1): P_n ≤ Q_n ≤ Q  т.е. P_n  ограничены и ряд Р сходится (§5).

   (2): P_n →∞ , Q_n ≥ P_n   Q_n →∞ и ряд Q расходится. }

Замечание. Неравенство  можно заменить на    

Пример. Исследовать на сходимость:  . { }

Предельный признак сравнения. Пусть существует   В этом случае:

1) С ≠ 0 : ряды P и Q  сходятся или расходятся одновременно.

2) С = 0 : из сходимости Q следует сходимость Р, а из расходимости  Р следует расходимость Q.

{ (1):   утверждение следует из ОПС.

 (2):    и снова  ОПС }

Предельный признак Коши. Пусть существует  .

Если s < 1 – ряд  Р сходится, если s > 1 – расходится. (при s = 1 вопрос о сходимости открыт).

{1.   По ОПС ряд P

сходится. 2. s > 1;  ряд  Р  расходится по необходимому признаку } 

Замечание. При использовании признака Коши, полезно помнить:

Предельный признак Даламбера. . Пусть существует 

Если s < 1 – ряд  Р сходится, если s > 1 – расходится. (при s = 1 вопрос о сходимости открыт)

Интегральный признак Коши.

 Пусть функция  f(x) ≥ 0   не возрастает при х ≥ 1. В этом случае   и  

сходятся  или расходятся одновременно.

Проинтегрируем эти неравенства от  (k – 1) до  k  и просуммируем по  k  от 2-х  до  n:

         Если интеграл сходится, то частичные суммы ограничены (левое

неравенство) и ряд сходится. Если интеграл расходится (к бесконечности!), то частичные суммы неограниченны (правое неравенство) и ряд расходится. В обратную сторону доказательство

аналогично.}