1.11 Розрахунок дисперсії сигналу помилки при випадкових впливах

При впливі стаціонарного випадкового сигналу на лінійну стійку систему на виході системи виникає також стаціонарний випадковий сигнал, який можна розглядати як перетворений вхідний сигнал. Перетворення вхідного сигналу проявляється в зміні його статистичних характеристик – дисперсій, спектральної густини та інших.

Реальні випадкові впливи, які діють на промислові об’єкти керування, досить різноманітні по своїм властивостям. Але, при деякій ідеалізації, можна виділити обмежену кількість типових випадкових впливів.

Білий шум з обмеженою шириною спектра

. (1.44)

Сигнали з експоненціальною кореляційною функцією і спектральною густиною

. (1.45)

Сигнали з експоненціально-косинусною кореляційною функцією, відповідна спектральна густина

. (1.46)

Нехай на систему діють випадкові збурення з відомими спектральними густинами . Задаючий вплив є також випадковий сигнал з спектральною густиною . Нехай впливи не корельовані між собою, тоді

. (1.47)

Звідси випливає, що

. (1.48)

Кожна з цих дисперсій може бути обрахована незалежно одна від одної по формулам, які в нашому випадку, при поданні на вхід випадкового сигналу, перешкоди і збурення мають вигляд:

(1.49)

(1.50)

(1.51)

Обчислимо дисперсію, яка спричинена дією вхідного впливу

Приведемо отриманий вираз до такого вигляду

.

Де відповідні значення поліномів рівні

Для знаходження даного інтеграла скористаємось наближеною формулою

(1.52)

Підставивши відповідні значення отримаємо

(1.53)

Обчислимо дисперсію, яка обумовлена дією завад

Аналогічно отримаємо ,

Де відповідні значення поліномів рівні

Підставивши отримані значення отримаємо

(1.54)

Обчислимо дисперсію, яка обумовлена дією збурення

Провівши відповідні спрощення отримаємо

,

де

Для приблизної формули не виведено, тому скористаємося наступною методикою

, (1.55)

де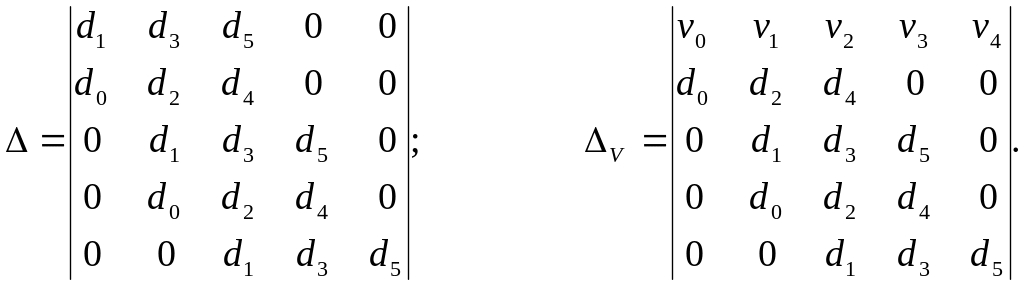 (1.56)

Тоді отримаємо

. (1.57)

Таким чином за отриманими формулами (1.53),(1.54) і (1.57), при відомій дисперсії сигналу і спектру сигналу можна визначити дисперсію сигналу помилки на виході системи.

2. Нелінійна система

2.1 Структура нелінійної системи

Автоматична система керування називається нелінійною, якщо хоча б один її конструктивний елемент описується нелінійним диференційним рівнянням. Практично всі реальні системи керування вміщують один або декілька нелінійних елементів. Нелінійною характеристикою часто наділений і керований об’єкт.

Структура нелінійної автоматичної системи в загальному випадку може бути досить складною. Степінь складності залежить від кількості, виду і методу включення нелінійних елементів. Зобразимо узагальнену алгоритмічну схему таких систем (рис.2.1)

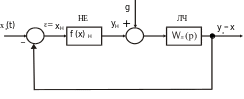
Рисунок 2.1 – Алгоритмічна схема нелінійної системи керування

. (2.1)

На схемі виділена лінійна частина ЛЧ і нелінійна частина НЕ.

Лінійна частина включає в себе всі лінійні ланки системи і може мати структуру будь-якої складності. Нелінійна частина утворена одним нелінійним елементом НЕ, вихідна величина якого може бути виражена як функція вхідної величини і її похідної

. (2.2)

Нелінійним елементом системи є елемент з статичною не лінійністю, заслінка, параметри якого

c=2; b=2;

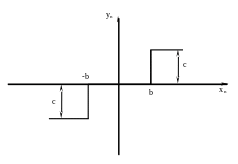
Рисунок 2.2 – Параметри нелінійного елемента

Рисунок 2.3 – Вихідна алгоритмічна схема