1.8 Побудова графіка перехідного процесу і оцінка якості системи

_{Якість автоматичної системи керування визначається сукупністю властивостей, які забезпечують ефективне функціонування як самого об’єкта керування, так і керуючого пристрою, тобто всієї системи керування в цілому.}

_{Точність системи в перехідних режимах оцінюють за допомогою прямих і непрямих показників.}

_{Прямі показники визначають по графіку перехідного процесу, що виникає в системі при ступеневому зовнішньому впливі. Одним із головних прямих показників якості є перерегулювання , що за каналом визначається за формулою}

_{, (1.34)}

_{де - відповідно перше максимальне відхилення від усталеного значення , і початкове значення.}

_{Тривалість перехідного процесу (час регулювання) - інтервал часу від моменту прикладання ступеневого впливу до моменту, після якого відхилення керованої величини від її кінцевого значення не перевищує деяке задане число . Як правило в промисловій автоматиці .}

_{Прямим показником якості служить і степінь затухання}

_{, (1.35)}

_{де А1 та А3 – сусідні максимальні відхилення амплітуди одного знаку. Щодо непрямих показників якості, то найважливіші серед них є частотний показник коливальності М, який визначається по АЧХ замкнутого контуру; запас стійкості по фазі та амплітуді.}

_{Всі задані показники якості нормуються.}

_{Побудуємо графік перехідного процесу по каналу Хз-Х (Рисунок 1.8) і визначимо показники якості системи.}

_{Для цього скористаємось програмою MathCAD.}

_{Визначимо прямі показники якості системи}

_{Час перехідного процесу}

_{Перерегулювання ;}

_{Степінь затухання .}

_{Отже дана система стійка так як перехідний процес регулювання затухає, але показники якості не відповідають заданим.}

_{З отриманих результатів можемо зробити висновок, про потребу коректуючого пристрою.}

_{Введемо у систему послідовний коректуючий пристрій, знаходження передавальної функції якого показане в розділі 1.9}

(1.36)

Після введення коректуючого пристрою структура АСК набуде вигляду

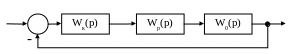
Рисунок 1.7 – Алгоритмічна структура скоректованої АСК

Знайдемо передавальну функцію скоректованої системи

. (1.37)

Підставивши відповідні значення, отримаємо

. (1.38)

Рисунок 1.8 – Перехідний процес нескоректованої АСК

По каналу

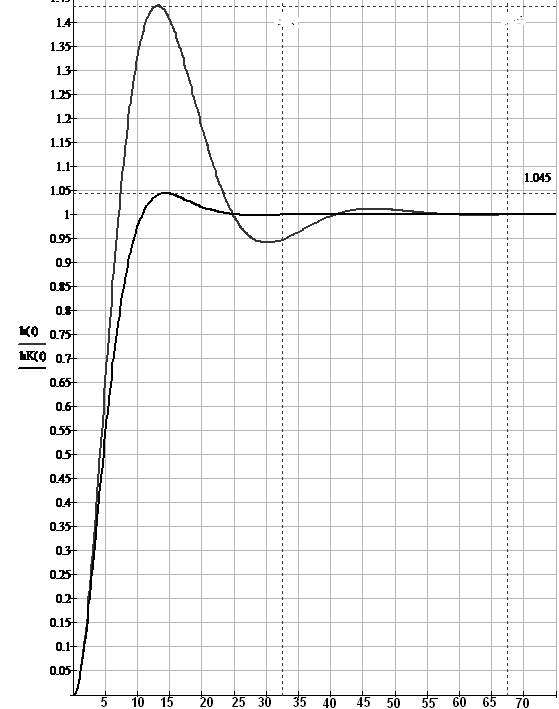
Рис. 1.9 - Перехідний процес скоректованої АСК

По каналу

Час перехідного процесу

Перерегулювання: .

Степінь затухання: .

Так, як час перехідного процесу скоректованої АСК зменшився вдвічі, пере регулювання зменшилось на 25%, збільшивсь степінь затухання, то можемо зробити висновок, що якість перехідного процесу значно збільшилася. При порівнянні з вимогами якості ( , ) бачимо вірність вибору коректуючого пристрою.

Перейдемо до визначення непрямих показників якості, основним з яких є частотний показник коливальності М.

Знайдемо його з графіка АЧХ передавальної функції замкнутого контуру. Для побудови графіка, спочатку знайдемо АФХ з передавальної функції скоректованої замкнутої системи (1.42), зробивши заміну . Тоді отримаємо

.

Для побудови АЧХ розділяємо отриманий вираз на дійсну і уявну частини

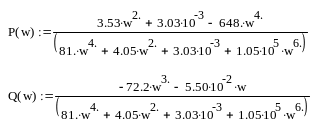
Звідси (1.33)

(1.34)

Для побудови скористаємося послугами програмного пакету MathCAD (Рисунок 1.8).

Аналізуючи графік можна прийти до висновку, що частотний показник коливальності рівний

Як бачимо частотний показник коливальності задовольняє нашій умові ( ).

Знайдемо запас стійкості по фазі та амплітуді.

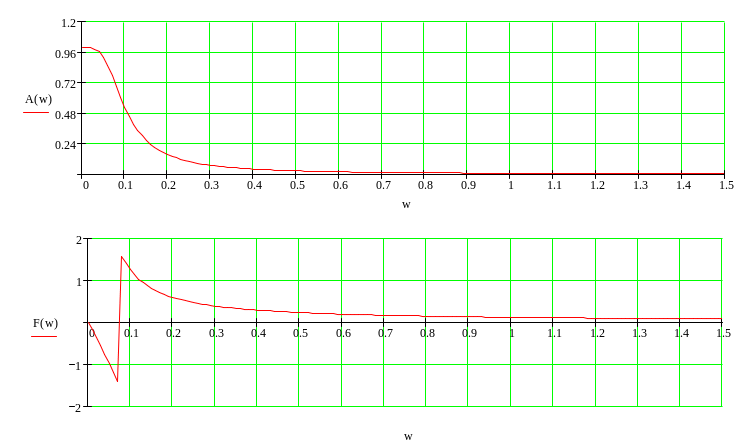
Рисунок 1.10 – Графіки АЧХ і ФЧХ скоректованої АСК

Визначення показників ґрунтується на аналізі АФХ розімкнутого контуру

. (1.35)

.

Зробивши заміну і розділивши отриманий вираз на дійсну і уявну частини, отримаємо

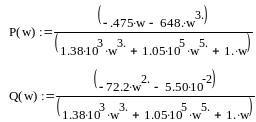
Для побудови АФХ скористаємося послугами програмного пакету MathCAD.

∆φ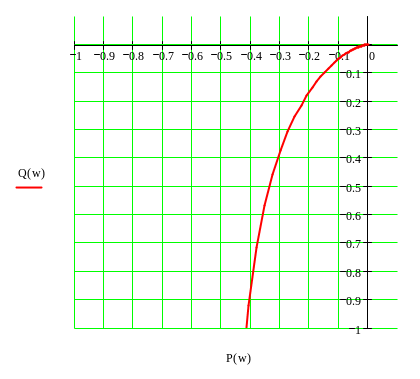

Рисунок 1.11 – Графік АФХ розімкнутої АСК

Аналізуючи графік можна прийти до таких висновків.

Запас стійкості по амплітуді .

Запас стійкості по фазі рівний , так як АФХ не перетинає одиничне коло.

Ці непрямі показники характеризують віддаленість кривої від критичної точки . При проектуванні систем для забезпечення доброї якості керування задаються запасом стійкості по амплітуді і по фазі . Як бачимо отримані нами значення задовольняють цим умовам.

Проаналізувавши всі показники якості можемо зробити такі висновки.

Якість скоректованої системи значно поліпшилась. Виходячи з значень запасів по амплітуді і фазі, стійкість системи також покращилася (зріс запас стійкості).

Таким чином система автоматичного керування відповідає всім вимогам якості.