1.4 Розрахунок оптимальних параметрів налаштування регулятора

Для вибору параметрів налаштування регулятора запишемо передавальну функцію розімкненої системи:

(1.4)

(1.5)

Виходячи з того, що дана САК містить астатичну ланку першого порядку, виберемо ПД – регулятор, що не вносить в систему астатизму і збільшить швидкодією, скомпенсувавши тим самим велику інертність АСК .

Використовуємо ПП «MATLAB» для вирішення задачі вибору параметрів налаштування регулятора

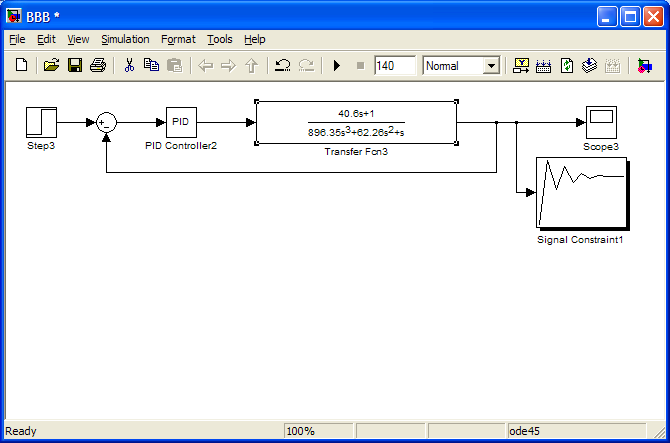
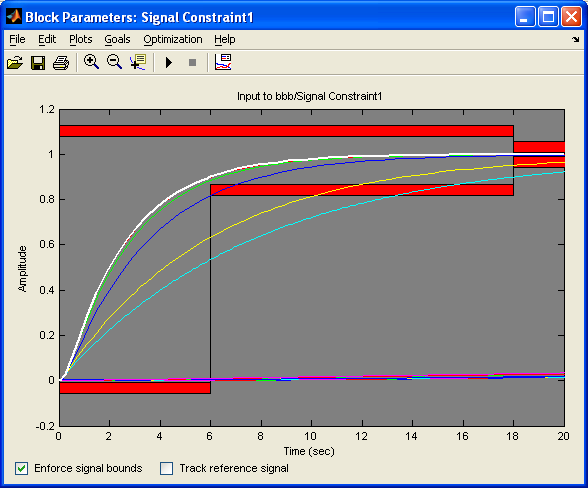
Рис. 1.4 – розрахунок параметрів налаштування регулятора методом параметричної оптимізації з використанням ПП «MATLAB»

В загальному випадку функція передачі ПД-регулятора:

(1.6)

Для нашого випадку він матиме вигляд:

(1.7)

Визначимо загальну передавальну функцію розімкнутої системи

(1.8)

(1.9)

1.5 Оцінка точності системи

Призначення будь-якої автоматичної системи управління – зміна вихідної величини у відповідності із зміною задаючого впливу . В більшості випадків це завдання системи полягає в підтриманні рівності при будь-яких змінах задаючого і збурюючого впливів.

При аналізі точності розрізняють дві функції системи:

• відтворення задаючого впливу;

• компенсація збурюючих впливів.

Через інерційність об’єкта і регулятора обидві ці функції виконуються будь-якою реальною системою з похибкою:

. (1.10)

Сигнал помилки можна розглядіти як суму двох складових:

. (1.11)

де - складова сигналу помилки, що характеризує точність відтворення з

задаючого впливу;

- складова сигналу помилки, що показує точність компенсації збурюючих впливів.

Розрізняють статичну і динамічну точності.

Статичну похибку оцінюють лише для статичних систем, в астатичній системі вона рівна нулю.

Для оцінки динамічної похибки скористаємось передавальною функцією розімкнутого контура (1.9)

Згідно умови маємо вплив виду , де .

Тоді згідно загального правила визначення похибко маємо. Порядок астатизму регулятора рівний одиниці. Порядок астатизму САК рівний 2.

Тобто ( ). Отже:

;

.

Як бачимо дана астатична САК 3-го порядку має не значну похибку на заданий вплив, і так як головним впливом є функція Хевісайда, то корекцію в систему вводити недоцільно.

1.6 Перевірка стійкості автоматичної системи керування

Однією з найважливіших характеристик автоматичної системи керування поряд з точністю є стійкість. Причому, якщо показники точності визначають степінь корисності і ефективності системи, то від стійкості залежить її працездатність.

Відповідно до завдання на курсову роботу, дослідимо стійкість системи за критеріями: Гурвіца і Михайлова.