Зміст

Вступ……………………………………………………………………………4

1. Лінійна система……………………………………………………………....5

1. Вихідні дані…………………………………………………………….....5

2. Визначення функції передачі керованого об’єкта…………………………………………………………………….8

3. Вибір регулятора………………………………………………………..10

4. Розрахунок оптимальних параметрів налаштування регулятора………………………………………………………………..10

5. Оцінка точності системи………………………………………………..12

6. Перевірка стійкості автоматичної системи керування…………………………………………………………………13

7. Побудова області стійкості системи…………………………………...15

8. Побудова графіка перехідного процесу і оцінка якості системи……………………………………………………………………19

9. Визначення функції передачі компенсуючого пристрою, який забезпечує інваріантність системи. Структура інваріантної системи.26

10. Інтегральна оцінка якості………………………………………….26

11. Розрахунок дисперсії сигналу помилки при випадкових впливах……………………………………………………………………29

2. Нелінійна система…………………………………………………………32

2.1 Структура нелінійної системи…………………………………………….32

2.2 Аналіз стійкості нелінійної системи…………………………………...33

2.3 Показники якості нелінійної системи…………………………………38

3. Цифрова система……………………………………………………………40

3.1 Структура цифрової системи…………………………………………..40

3.2 Аналіз стійкості системи……………………………………………….41

3.3 Аналіз якості системи…………………………………………………..42

Висновок…………………………………………………………………….45

Список літературних джерел……………………………………………….46

ВСТУП

Теорія автоматичного керування(ТАК) – наукова дисципліна, предметом вивчення якої являються інформаційні процеси, що протікають в автоматичних системах керування. ТАК виявляє загальні закономірності функціонування, притаманні автоматичним системам різної фізичної природи, і на основі цих закономірностей розробляються принципи побудови високоякісних систем керування.

В даний час ТАК поряд з новими розділами так званої загальної теорії керування (дослідження операцій, системотехніка, теорія ігор, теорія масового обслуговування) відіграє важливу роль у вдосконаленні і автоматизації керування виробництвом.

Для здійснення автоматичного керування технічними процесами створюється система, що складається із керованого об’єкта і зв’язаного з ним керуючого пристрою. Система повинна володіти конструктивною жорсткістю і динамічною міцністю, тобто система повинна виконувати задані їй функції з необхідною точністю, не дивлячись на інерційні властивості і на неменучі перешкоди. Поки об’єкт володіє достатньою жорсткістю і динамічною міцністю, потреби в автоматичному регулюванні не виникають.

1 Лінійна система

1.1 Вихідні дані

В курсовій роботі необхідно виконати комплекс розрахунків автоматичної системи керування, яка задана у вигляді узагальненої уніфікованої алгоритмічної схеми (рисунок 1.1).

Рис.1.1 - Узагальнена уніфікована алгоритмічна схема автоматичної системи керування

Автоматична система складається з керованого об’єкту КО, виконавчого механізму ВМ, автоматичного керуючого пристрою АКП, одного коректуючого пристрою КП, який включено зустрічно-паралельно в контур системи. ВМ може розглядатися як ідеальна інерційна ланка першого порядку.

Передавальна функція керованого об’єкту визначається на підставі вивчення і побудови заданих перехідних характеристик. Система керування спочатку розглядається як лінійна з лінійним перетворюючим елементом ПЕ, а потім як нелінійна з нелінійним елементом НЕ і цифрова з імпульсним елементом ІЕ.

Передавальні функції об’єктів:

;

;

;

.

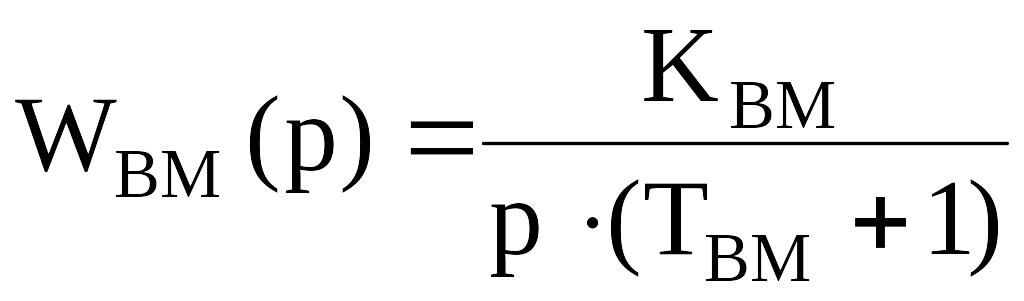Вихідна величина Х (керована величина) системи залежить від керуючого впливу Y і збурюючого впливу Z. Необхідний закон зміни величини X визначається задаючим впливом X_з. Крім основного збурюючого впливу Z на систему діє завада q. Внаслідок впливу цих збурень, а також інерційності елементів системи в перехідних і усталених режимах, в системі виникає сигнал відхилення Е, який називається сигналом помилки.

Таблиця 1.1 – Параметри лінійних елементів системи

КО		ВМ		ПЕ	ВП
	, с		, с
0.2	1.1	1.0	-	0.9	1.1

Таблиця 1.2 – Параметри зовнішніх збурень, показників якості системи

Параметри впливу
		В усталеному режимі		В перехідному процесі
				, %	,с	М
-	2.0	0.50	0.10	25	3.1	1.30

Таблиця 1.3 – Параметри стійкості і якості системи

Критерій	Область стійкості по параметрах	Показники якості по каналу
Гурвіца, Михайлова	і

;

;

.

Результати експерименту подано в таблиці 1.4.

t, c	0	10	20	30	40	50	60	70	80	90	100
	3	3	3	3	3	3	3	3	3	3	3
	0	32	47	58	68	71	75	77	79	80	80

Таблиця 1.4 – Результати експерименту

t, c	110	120	130	140	150	160	170	180	190	200
	3	3	3	3	3	3	3	3	3	3
	80	80	80	80	80	80	80	80	80	80

Дані відповідають варіанту №11 ( залікова книжка №003).

Маючи ці дані ми можемо зобразити перехідний процес в для цього використаємо середовище MatCad

Рис.1.2 - Перехідна характеристика процесу