Связь между комплексным коэффициентом передачи и временной характеристикой аср. Частотные характеристики разомкнутых и замкнутых систем управления. Понятие системы не минимальной фазы.
При исследовании и проектирования автоматических систем обычно используют амплитудно-фазовые (АФЧХ) и логарифмические частотные характеристики (ЛЧХ) разомкнутых одноконтурных систем. Их передаточные функции W(s) легко могут быть преобразованы к виду
,
где Wi(s) – передаточные функции элементарных звеньев. В этом случае модули и аргументы частотных передаточных функций системы и звеньев
, 
, 
, 
связаны между собой соотношениями
,
(3.60)
.
(3.61)
Вещественные и мнимые частотные функции системы определяются равенствами
.
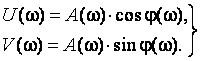(3.62)
Пользуясь соотношениями
(3.60-3.62), можно построить АФЧХ – W(j
).
Логарифмическая амплитудная частотная характеристика (ЛАЧХ) из (3.60) записывается в виде:
Для анализа и синтеза САР (в частности, многоконтурных) может понадобится нахождение ЛАЧХ и ЛФЧХ замкнутой системы по известным ЛАЧХ и ЛФЧХ разомкнутой системы.
АФЧХ замкнутой системы в соответствии с главной передаточной функцией (3.49) при единичной обратной связи имеет вид:
Ф
.
(3.64)
Она может быть представлена в виде
Ф
,
(3.65)
где P(w) и Q(w) называются вещественной и мнимой частотными характеристиками замкнутой системы.
Представив исходную АФЧХ разомкнутой цепиW(jw) в виде
(3.66)
и подставив ее в формулу (3.65), найдем
.
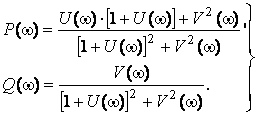(3.67)
Линии P=const и Q=const оказываются окружностями на плоскости (U,V). На основании этого строится круговая номограмма. Наложив на поле этой номограммы заданную АФЧХ разомкнутой цепи W(jw), построенную в координатахU(w) и V(w), в точках пересечения ее с окружностями P=const и Q=const, получим значения вещественной P(w) и мнимой Q(w) частотных характеристик замкнутой системы [ 2 ].
Номограммы применимы для систем, имеющих единичную обратную связь. Если система имеет неединичную обратную связь, то передаточная функция системы в замкнутом состоянии имеет вид (см. рис. 3.20)
Ф 
.
(3.68)
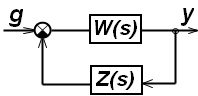
Рис. 3.20. Схема системы с неединичной обратной связью
Для применения номограмм или построения ЛАЧХ замкнутой системы в этом случае следует представить передаточную функцию Ф(s) следующим образом:
Ф
.
(3.69)
Выражение в квадратных скобках дает возможность воспользоваться номограммой из [ 2 ] и найти ЛАЧХ, соответствующую этому выражению. Из полученной ЛАЧХ следует вычесть ЛАЧХ, соответствующую передаточной функции Z(s).
В результате получается ЛАЧХ замкнутой системы с неединичной обратной связью:
.
(3.70)
При построении ЛАЧХ можно воспользоваться следующими соотношениями:
Когда 
, 
;
(3.71)
если
, 
.
(3.72)
Отсюда следует определение не минимальной фазовой системы: в теории управления и цифровой обработки сигналов линейная, постоянная во времени система является не минимально фазовой, если система и ее отображение не существуют и не стабильны.
Модели многомерных объектов управления. Матричная операторная передаточная функция оу.
У многомерных объектов математическая модель содержит несколько управляющих и несколько управляемых координат.
Отличительной особенностью реальных многомерных многосвязных объектов является то, что каждая выходная, управляемая величина зависит не от одной, а от нескольких входных, управляющих величин, а также нескольких возмущений. Управление таким объектом может оказаться довольно сложной задачей.
Матричная
передаточная функция от вектора входа
системы 
до
вектора выхода 
—
это матрица 
,
элемент 
-й
строки 
-го
столбца представляет собой передаточную
функцию системы от
-й
координаты вектора входа системы до
-й
координаты вектора выхода.