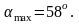- •С.В. Шапиро Курс физики Учебное пособие
- •Рецензенты:
- •Содержание
- •Раздел 1. Механика……………………………………...……….………………..8
- •Раздел 2. Термодинамика..……………………………………………………...45
- •Раздел 3. Электричество и магнетизм………………………………………...86
- •Раздел 5. Физические основы строения материи…………………………..175
- •Цель и задачи курса
- •Раздел первый. Механика глава первая. Кинематика
- •1.1. Материальная точка и основные характеристики ее движения
- •Декартовой системе координат
- •1.2. Вращательное движение материальной точки
- •Векторное изображение угловой скорости (б)
- •1.3. Кинематика твердого тела. Разложение произвольного движения на поступательное и вращательное
- •1.4. Относительное движение
- •1.5. Релятивистские эффекты в кинематике
- •Масштаба длины (в)
- •Вопросы по первой главе:
- •Глава вторая. Динамика
- •2.1. Взаимодействие материальных точек. Понятие силы
- •2.2. Законы статики изолированного множества материальных точек
- •1 Закон статики.
- •2 Закон статики.
- •2.3. Закон сохранения импульса изолированного множества материальных точек. Центр масс
- •2.4. Закон сохранения момента импульса изолированного множества материальных точек. Теорема Штейнера
- •2.5. Работа, энергия, закон сохранения энергии
- •Материальной точки Mq: а, б – под действием одной материальной точки Mp;
- •2.6. Взаимодействие двух изолированных множеств материальных точек
- •2.7. Связи абсолютно-твердых тел
- •2.8. Релятивистская масса
- •2.9. Гравитационное взаимодействие
- •2.10. Динамика упругого тела
- •Вопросы по второй главе:
- •Раздел II. Термодинамика глава третья. Идеальный газ
- •3.1. Основные характеристики идеального газа
- •Движением всех корпускул, входящих в газ (а), их упорядоченным движением (б) и в промежуточной ситуации (в)
- •3.2. Уравнение состояния Менделеева–Клапейрона
- •3.3. Работа идеального газа. Теплота и внутренняя тепловая энергия. Первый закон термодинамики
- •3.4. Энтропия. Второй принцип термодинамики
- •Аналогично для второго газа записываем
- •Если принять отношения
- •3.5. Адиабатические, изотермические, изохорические, изобарические процессы
- •3.6. Неравновесные системы
- •При теплообмене: 1 – источник тепловой энергии; 2 – приемник тепловой энергии (холодильник); 0 – объем идеального газа (открытая система)
- •Риc. 3.7. К раcчёту процесса преобразования теплового движения в упорядоченное в простейшей неравновесной системе
- •3.7. Цикл Карно
- •3.8. Распределение молекул газа по скоростям
- •Вопросы по третьей главе:
- •Глава четвёртая. Реальный газ и основы кинетики газа
- •4.1. Уравнение Ван дер-Ваальса
- •4.2. Столкновения молекул. Средняя длина свободного пробега. Скорость дрейфа
- •При столкновении корпускул идеального газа
- •Модель движения материальной точки под действием постоянной силы в условиях дескретно – повторяющегося столкновения с препятствиями (б) и зависимость V(τ) для такого движения
- •4.3. Явления переноса в газе
- •4.4. Диффузия газов
- •4.5. Теплопроводность
- •4.6. Внутреннее трение в газах (вязкость)
- •4.7. Основы аэро- и гидродинамики. Возникновение вихрей
- •В сплошной среде (б, в)
- •Вопросы по четвертой главе:
- •Раздел третий. Электричество и магнетизм глава пятая. Электростатика
- •5.1. Закон Кулона
- •Электрического взаимодействия; б – воздействие (n-1) зарядов на заряд qN;
- •5.2. Электрическое поле и его основные характеристики
- •И эквипотенциальными поверхностями (а) и поток вектора напряженности через инфинитезимальную поверхность (б)
- •5.3. Теорема Гаусса–Остроградского
- •5.4. Примеры применения теоремы Гаусса–Остроградского
- •Бесконечной длины: а – выбор замкнутой поверхности;
- •5.5. Электростатическое поле в диэлектрике
- •5.6. Электростатическая индукция. Теорема Гаусса-Остроградского для поля в разнородной среде
- •В разнородной среде
- •5.7. Энергия электростатического поля
- •Вопросы по пятой главе:
- •Глава шестая. Магнетизм
- •6.1. Взаимодействие движущихся зарядов и проводников с токами
- •С движущимися электронами; б – иллюстрация закона Био-Савара-Лапласа
- •6.2. Основные характеристики магнитного поля.
- •6.3. Закон полного тока
- •Магнитное поле торроидальной катушки
- •6.5. Электромагнитная индукция
- •Наводимого электромагнитной индукцией потока
- •6.6. Пара-, диа- и ферромагнетики
- •6.7. Явление взаимоиндукции. Идеальный трансформатор
- •Его схематическое изображение (б)
- •6.8. Энергия магнитного поля
- •Вопросы по шестой главе:
- •Глава седьмая. Электрический ток
- •7.1. Основные элементы цепи постоянного тока. Законы Ома и Джоуля–Ленца
- •7.2. Законы Кирхгофа для разветвленной цепи
- •(К описанию законов Кирхгофа)
- •7.3. Переменный синусоидальный ток
- •Векторами: а – единичный вектор во вращающейся системе координат;
- •7.4. Переменная синусоидальная эдс. Законы Ома и Кирхгофа в комплексном виде
- •И участок цепи синусоидального тока (в)
- •7.5. Переходные процессы в электрических цепях
- •Вопросы по седьмой главе:
- •Глава восьмая. Электромагнитное поле
- •8.1. Уравнения Максвелла
- •8.2. Теорема Умова–Пойнтинга
- •Двухпроводной линии (а) и круглого провода (б)
- •8.3. Плоское электромагнитное поле в диэлектрике
- •Плоской электромагнитной волны в диэлектрике
- •П(х); г – формирование е0(х)
- •8.4. Плоское синусоидальное электромагнитное поле в диэлектрике
- •8.5. Плоская электромагнитная волна в проводящей среде
- •8.6. Плоское синусоидальное электромагнитное поле в смешанной среде
- •8.7. Сферическое электромагнитное поле в диэлектрике
- •Вопросы по восьмой главе:
- •Для выбора основных цветов:1 – красный;2 – зелёный;3 – синий
- •9.2. Интерференция света
- •Монохроматических волн; в – интерференция сферических волн
- •Предмета на фотоплёнку при облучении его лазером (монохроматическим когерентным светом;б)получение объёмного (стереоскопического) изображения этого предмета
- •9.3. Дифракция света
- •9.4. Отражение и преломление волн на границе двух сред
- •9.5. Геометрическая оптика
- •Вопросы по девятой главе:
- •Глава десятая. Акустика
- •10.1. Акустические волны в газе. Волновое уравнение
- •10.2. Поперечные упругие колебания протяжённых твердых тел и поверхностей жидкостей
- •10.3. Распространение гармонического звука в газе
- •10.4. Негармонические звуковые колебания
- •Вопросы по десятой главе:
- •Раздел пятый. Физические основы строения материи глава одиннадцатая. Элементы квантовой механики
- •1.1. Принцип неопределенности
- •11.2. Волна вероятности. Уравнение Шредингера
- •Вероятность её нахождения вдоль оси X(б)
- •11.3. Волна вероятности ускоряющейся частицы. Волновой пакет
- •При ускорении частицы (а) и его структура (б)
- •11.4. Движение электрического заряда в центрально-симметричном электрическом поле
- •А) при числе эпициклов,равном 1; б) при числе 2
- •Вопросы по одиннадцатой главе:
- •Глава двенадцатая. Физические основы строения материи
- •12.1. Элементарные частицы
- •Камере в результате столкновения π ––мезона с протоном р(а). В результате реакции появились k0 – мезон и λ0 – гиперон.Они на фотографии
- •12.2. Модели ядра
- •12.3. Ядерные процессы
- •12.4. Структура атома. Энергетические уровни
- •12.5. Некоторые физические явления, обусловленные квантовыми процессами в атомах
- •12.6. Формирование молекулярных структур
- •Атомов от расстояния между их центрами
- •12.7. Агрегатные состояния вещества
- •12.8. Твердое тело
- •Двух молекул от расстояния между ними
- •В кристаллах
- •Вопросы по двенадцатой главе:
- •Приложения
- •Примеры решения задач Несколько советов
- •Несколько предварительных замечаний
- •1. Кинематика.
- •2. Статика Задача № п.2
- •Решение
- •3. Динамика Задача № п.3
- •Решение
- •4. Термодинамика Задача№ п.4
- •Решение
- •5. Электростатика Задача № п.5
- •Решение
- •6. Магнитное поле Задача № п.6
- •Решение
- •7. Электрический ток Задача № п.7
- •Решение
- •8. Переменное электромагнитное поле Задача № п.8
- •Решение
- •9. Акустика Задача № п.9
- •Решение
- •10. Оптика Задача № п.10
- •Решение
- •11. Атомная и ядерная физика Задача № п.11
- •Решение
- •12. Молекулы и кристаллы Задача № п.12
- •Решение
- •Некоторые сведения из векторного анализа
- •Международная система единиц
- •3.1. Основные единицы и их эталоны
- •3.2. Единицы механических величин
- •П.3.3. Единицы тепловых величин
- •3.4. Единицы электромагнитных величин.
- •3.5. Единицы электромагнитного излучения и освещенности
- •Основные хронологические даты истории физики
- •Приложение 5 основные физические константы
- •Список литературы
- •Шапиро Семен Валентинович
- •450078, Г. Уфа, ул. Чернышевского, 145, к. 206; тел. (347) 241-69-85.
Несколько предварительных замечаний
1. Ниже приведено по одной задаче с решением на каждую главу учебного пособия.
2. Задачи выбирались средней тяжести. Поэтому рекомендую сначала попробовать решить задачу самостоятельно по предложенной выше процедуре и лишь при возникновении трудностей ознакомиться с предложенным решением.
3. При выборе исходных формул здесь, естественно, не соблюдается рекомендация п. 3 «Советов…» об избыточности: выписываются только те формулы, которые используются при решении.
1. Кинематика.
Задача № П.1
Мяч
падает вертикально с высоты 10 метров
на склон оврага, составляющего угол
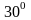 с
горизонтальной осью. После упругого
отражения он снова падает на этот склон,
после чего снова отскакивает и т. д.
Сколько времени пройдет между первым
и вторым падениями мяча? (Трением мяча
о воздух пренебречь, начальная скорость
мяча равна нулю).
с
горизонтальной осью. После упругого
отражения он снова падает на этот склон,
после чего снова отскакивает и т. д.
Сколько времени пройдет между первым
и вторым падениями мяча? (Трением мяча
о воздух пренебречь, начальная скорость
мяча равна нулю).
Решение
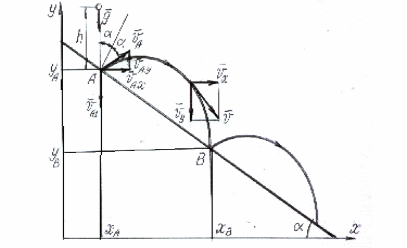
Рис. П.1
На рис. П.1 дано схематическое изображение ситуации задачи. Овраг изображён наклонной линией, помещенной в систему координат [Х,У] и образующей с осью х угол
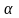 .
Мяч изображен точкой, падающей вертикально
с высоты h
в точку А
наклонной
линии и отскакивающей от нее под тем
же углом к перпендикуляру АС,
который составляла с ним до отражения
траектория её падения. Траектория
движения точки, изображающей мяч, после
отскока – АМВ,
завершается в точке В.
На этой же схеме нанесены координаты
точек А и
В
– [xA,
уA],
[xB,
уB],
векторы скорости мяча в т.
А
до отражения и после отражения
.
Мяч изображен точкой, падающей вертикально
с высоты h
в точку А
наклонной
линии и отскакивающей от нее под тем
же углом к перпендикуляру АС,
который составляла с ним до отражения
траектория её падения. Траектория
движения точки, изображающей мяч, после
отскока – АМВ,
завершается в точке В.
На этой же схеме нанесены координаты
точек А и
В
– [xA,
уA],
[xB,
уB],
векторы скорости мяча в т.
А
до отражения и после отражения
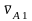 и
и
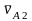 ,
проекции
,
проекции
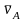 -
-
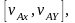 ускорение
земного притяжения мяча
g,
скорость мяча в промежуточной точке
траектории М
-
ускорение
земного притяжения мяча
g,
скорость мяча в промежуточной точке
траектории М
-
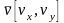 .
Здесь же показано, что углы падения и
отражения мяча в точке А
с перпендикуляром
АС
также равны
,
так как стороны первого из них составляют
900
со сторонами исходного угла.
.
Здесь же показано, что углы падения и
отражения мяча в точке А
с перпендикуляром
АС
также равны
,
так как стороны первого из них составляют
900
со сторонами исходного угла.h=10м
=300
tAB= t =?
3. Формулы кинематики
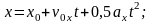
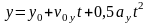 ;
;
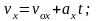
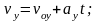
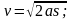
Формулы тригонометрии
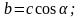 (с
– гипотенуза,
а
– противолежащий
катет, b
– прилежащие
к углу α
катет).
Константа g=9,8м/с2
(с
– гипотенуза,
а
– противолежащий
катет, b
– прилежащие
к углу α
катет).
Константа g=9,8м/с2
4. Составляем систему уравнений:
1)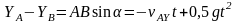
2)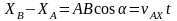
3)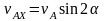
4)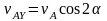
5)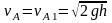
Уравнений –5, неизвестных тоже 5:
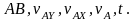
Делим 1) на 2):
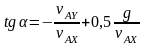
Подставляем
 из 3), 4), 5) уравнений
из 3), 4), 5) уравнений
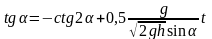
Находим t:
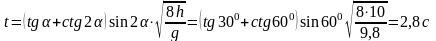
Ответ: tAB=2,8c
2. Статика Задача № п.2
Лестница длиной 5 м массой 15 кг наклонно прислонена к вертикальной стенке и по ней поднимается человек массой 70 кг. Под каким минимальным углом к горизонтальному полу можно поставить лестницу, чтобы она не начала скользить под весом человека, если коэффициент трения между ней и полом 0,5, по стенке она скользит без трения, а человек поднимается по ней на длину 4 м.
Решение
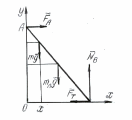
Рис. П.2
1. На рис. П.2 отрезком
прямой АВ изображена лестница,
установленная наклонно (под углом
к
оси х) между вертикальной стеной
(ось у) и полом (ось х). Ее
вес изображен вектором
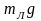 посредине. На лестнице точкой обозначен
поднявшийся до точки С человек.
Его вес mg указан
вектором на удалении от пола на расстояние
ВС векторами
посредине. На лестнице точкой обозначен
поднявшийся до точки С человек.
Его вес mg указан
вектором на удалении от пола на расстояние
ВС векторами
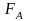 и
NВ
изображены силы реакции стены и пола
на давление лестницы. Обе они
перпендикулярны к соответствующим
поверхностям. Вектор
и
NВ
изображены силы реакции стены и пола
на давление лестницы. Обе они
перпендикулярны к соответствующим
поверхностям. Вектор
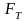 означает силу трения лестницы пол. Для
того чтобы лестница устойчиво стояла,
эта сила должна быть не больше, чем
произведение
означает силу трения лестницы пол. Для
того чтобы лестница устойчиво стояла,
эта сила должна быть не больше, чем
произведение
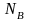 на коэффициент трения
на коэффициент трения
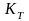 .
.
АВ=5м.
ВС=4м.
m=70кг.
mЛ=15кг.
=0,5
3. Формулы статики
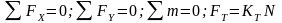
Формулы тригонометрии
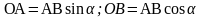
Константа
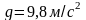
4. Составляем систему уравнений
1)
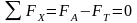
2)
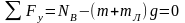 ;
;
3)
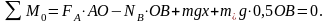
4)
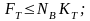
5)
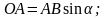
6)
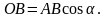
Шесть
уравнений и шесть неизвестных (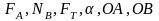 ),
),
Подставляем 1), 2), 5), 6) уравнения в 3):
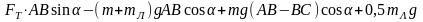
Получаем
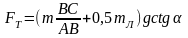
Из формул 2) и 4) находим
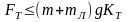
Следовательно
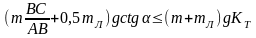
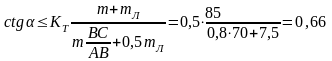
Ответ: